该芯片是基于一个16位查找表实现的,电路需要最小 2 16
我们的目标是使约束的度数最大为9。这让我们能够在同一行内处理进位的约束,以及对一些 { 0..7 }
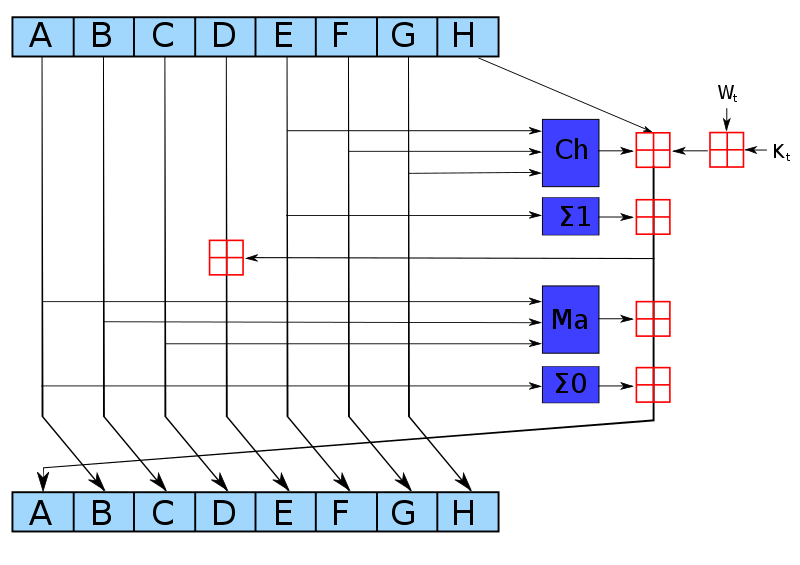
总共有64个 compression 轮次。每轮使用8个32位数 A , B , C , D , E , F , G , H
C h ( E , F , G ) M aj ( A , B , C ) Σ 0 ( A ) Σ 1 ( E ) H ′ E n e w A n e w = = = = = = = = ( E ∧ F ) ⊕ ( ¬ E ∧ G ) ( A ∧ B ) ⊕ ( A ∧ C ) ⊕ ( B ∧ C ) co u n t ( A , B , C ) ≥ 2 ( A ⋙ 2 ) ⊕ ( A ⋙ 13 ) ⊕ ( A ⋙ 22 ) ( E ⋙ 6 ) ⊕ ( E ⋙ 11 ) ⊕ ( E ⋙ 25 ) H + C h ( E , F , G ) + Σ 1 ( E ) + K t + W t re d u c e 6 ( H ′ + D ) re d u c e 7 ( H ′ + M aj ( A , B , C ) + Σ 0 ( A ))
re d u c e i 0 ≤ carry < i
定义 spread spread
我们注意到模 2 32 a b
a ⊞ b = c ,
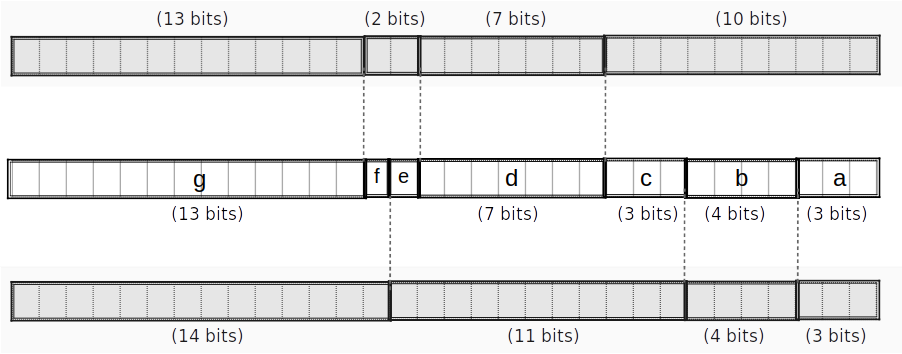
我们将操作数分解为16位一个的 chunks :
( a L : Z 2 16 , a H : Z 2 16 ) ⊞ ( b L : Z 2 16 , b H : Z 2 16 ) = ( c L : Z 2 16 , c H : Z 2 16 ) ,
然后使用有限域的加法重新定义约束:
carry ⋅ 2 32 + c H ⋅ 2 16 + c L = ( a H + b H ) ⋅ 2 16 + a L + b L .
更一般化的,输出可以被分解为任意的比特位组合,而不仅仅是16位一组的 chunks 。注意上述等式已经正确处理了从 a L + b L
约束要求每个 chunk 都是在正确范围内的,否则之后的赋值可能会导致有限域上的溢出。
操作数和结果的 chunk 可以通过 spread ⊞ A n e w ⊞ E n e w M aj C h
carry small range constraint 来进行约束。
M aj 4 2 spread ∗ 2
正如之前提到的,在第一轮之后我们已经有了了 A A ′ B C A B B ′ C ′ spread
在域中添加 spread 形式:M ′ = A ′ + B ′ + C ′
我们可以以 32位计算机字的形式或者以片(piece) 的形式添加,两者是等价的
对于 i = { 0..1 } M i e v e n M i o dd
将 M ′ M ′ = spread ( M 0 e v e n ) + 2 ⋅ spread ( M 0 o dd ) + 2 32 ⋅ spread ( M 1 e v e n ) + 2 33 ⋅ spread ( M 1 o dd ) M i o dd M aj
注意:“偶数位”指的是 2 2
TODO: can probably be optimized to 4 5
C h 8 4 spread ∗ 2
如之前所提到的,在第一轮之后我们已经有了 E E ′ F G E F F ′ G ′ spread
计算 P ′ = E ′ + F ′ Q ′ = ( e v e n s − E ′ ) + G ′ e v e n s = spread ( 2 32 − 1 )
我们可以以 32位计算机字的形式或者以片(piece)的形式添加,两者是等价的
e v e n s − E ′ ¬ E spread E ′ 1
计算 P i e v e n , P i o dd , Q i e v e n , Q i o dd P ′ = spread ( P 0 e v e n ) + 2 ⋅ spread ( P 0 o dd ) + 2 32 ⋅ spread ( P 1 e v e n ) + 2 33 ⋅ spread ( P 1 o dd ) Q ′
{ P i o dd + Q i o dd } i = 0..1 C h
Σ 0 ( A ) 6
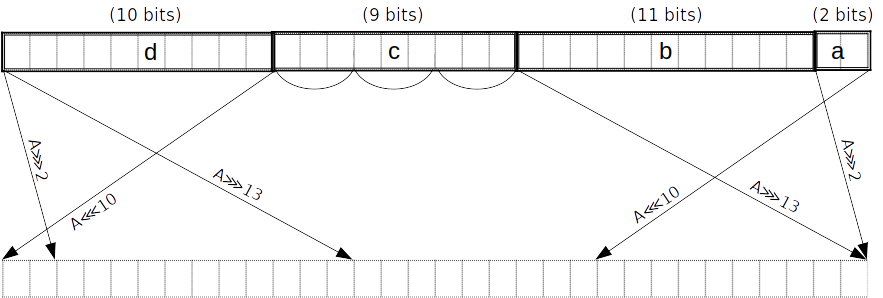
我们首先将 A ( 2 , 11 , 9 , 10 ) ( a , b , c , d ) spread
注意到将 chunk 划分为片可以和 A n e w A n e w
( A ⋙ 2 ) ⊕ ( A ⋙ 13 ) ⊕ ( A ⋙ 22 ) ( A ⋙ 2 ) ⊕ ( A ⋙ 13 ) ⊕ ( A ⋘ 10 )
然后,使用 4 spread R ′
R ′ = ( a ( b ( c 4 30 a 4 21 b 4 23 c ∣∣ ∣∣ ∣∣ + + + d a b 4 20 d 4 19 a 4 12 b ∣∣ ∣∣ ∣∣ ⇓ + + + c d a 4 11 c 4 9 d 4 10 a ∣∣ ∣∣ ∣∣ + + + b ) c ) d ) b c d ⊕ ⊕ + +
即,我们计算出压缩后的偶数位 R i e v e n R i o dd
R ′ = spread ( R 0 e v e n ) + 2 ⋅ spread ( R 0 o dd ) + 2 32 ⋅ spread ( R 1 e v e n ) + 2 33 ⋅ spread ( R 1 o dd )
其中 { R i e v e n } i = 0..1 Σ 0
Σ 1 ( E ) 6
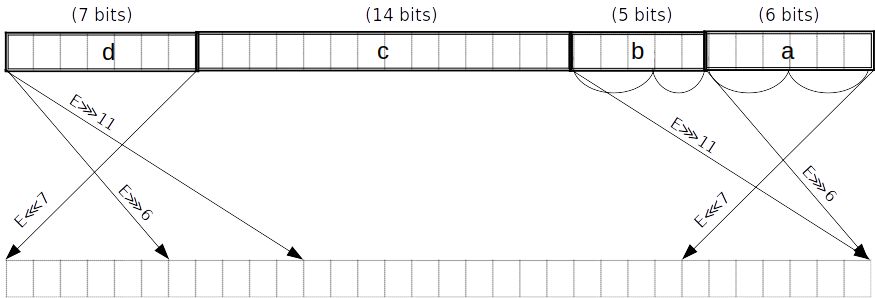
我们首先将 E ( 6 , 5 , 14 , 7 ) ( a , b , c , d ) spread
注意到将 chunk 划分为片可以和 E n e w E n e w
( E ⋙ 6 ) ⊕ ( E ⋙ 11 ) ⊕ ( E ⋙ 25 ) ( E ⋙ 6 ) ⊕ ( E ⋙ 11 ) ⊕ ( E ⋘ 7 )
然后,使用 4 spread R ′
R ′ = ( a ( b ( c 4 26 a 4 27 b 4 18 c ∣∣ ∣∣ ∣∣ + + + d a b 4 19 d 4 21 a 4 13 b ∣∣ ∣∣ ∣∣ ⇓ + + + c d a 4 5 c 4 14 d 4 7 a ∣∣ ∣∣ ∣∣ + + + b ) c ) d ) b c d ⊕ ⊕ + +
即,我们计算出压缩后的偶数位 R i e v e n R i o dd
R ′ = spread ( R 0 e v e n ) + 2 ⋅ spread ( R 0 o dd ) + 2 32 ⋅ spread ( R 1 e v e n ) + 2 33 ⋅ spread ( R 1 o dd )
其中 { R i e v e n } i = 0..1 Σ 1
对于消息中每一个512位的块 M ∈ { 0 , 1 } 512 64 32
前 16 M M = W 0 ∣∣ W 1 ∣∣ ⋯ ∣∣ W 14 ∣∣ W 15 ;
剩下的 48 W i = σ 1 ( W i − 2 ) ⊞ W i − 7 ⊞ σ 0 ( W i − 15 ) ⊞ W i − 16 , 16 ≤ i < 64
Note: W 0
σ 0 ( X ) σ 1 ( X ) = = ( X ⋙ 7 ) ⊕ ( X ⋙ 18 ) ⊕ ( X ≫ 3 ) ( X ⋙ 17 ) ⊕ ( X ⋙ 19 ) ⊕ ( X ≫ 10 )
Note: ≫ 移位 运算,不是循环,和 ⋙
( X ⋙ 7 ) ⊕ ( X ⋙ 18 ) ⊕ ( X ≫ 3 ) ( X ⋙ 7 ) ⊕ ( X ⋘ 14 ) ⊕ ( X ≫ 3 )
和之前类似,也用小数端表示,但 ( a , b , c , d ) ( 3 , 4 , 11 , 14 ) b
R ′ = ( 0 [ 3 ] ( b ( c 4 28 b 4 21 c ∣∣ ∣∣ ∣∣ + + d a b 4 15 d 4 25 a 4 17 b ∣∣ ∣∣ ∣∣ ⇓ + + + c d a 4 4 c 4 11 d 4 14 a ∣∣ ∣∣ ∣∣ + + + b ) c ) d ) b c d ⊕ ⊕ + +
( X ⋙ 17 ) ⊕ ( X ⋙ 19 ) ⊕ ( X ≫ 10 ) ( X ⋘ 15 ) ⊕ ( X ⋘ 13 ) ⊕ ( X ≫ 10 )
TODO: this diagram doesn't match the expression on the right. This is just for consistency
with the other diagrams.
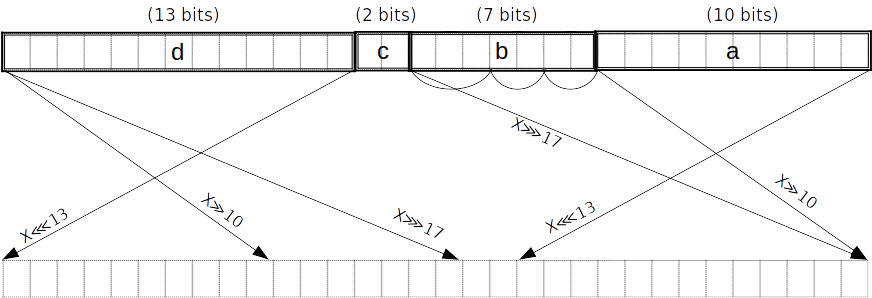
和之前一样用小数端表示, ( a , b , c , d ) ( 10 , 7 , 2 , 13 ) b ( 3 , 2 , 2 )
R ′ = ( 0 [ 10 ] ( b ( c 4 25 b 4 30 c ∣∣ ∣∣ ∣∣ + + d a b 4 9 d 4 15 a 4 23 b ∣∣ ∣∣ ∣∣ ⇓ + + + c d a 4 7 c 4 2 d 4 13 a ∣∣ ∣∣ ∣∣ + + + b ) c ) d ) b c d ⊕ ⊕ + +
我们将 σ 0 W 1..48 σ 1 W 14..61 spread W 14..48 ( 3 , 4 , 11 , 14 ) ( 10 , 7 , 2 , 13 ) ( 3 , 4 , 3 , 7 , 1 , 1 , 13 )
如果我们可以将合并后的分解在3行中完成(单独分解 σ 0 σ 1
These might even be doable in 2
我们可以将 W 16..61 2 32 A E
我们仍然需要对 W 62..63 A n e w E n e w
优化后的调度结果为:
2 W 0 32
技术上这不是必须的,这里进行约束是保持鲁棒性,因为输入部分的约束是免费的
13 ∗ 2 W 1..13 ( 3 , 4 , 11 , 14 ) 35 ∗ 3 W 14..48 ( 3 , 4 , 3 , 7 , 1 , 1 , 13 ) W 14..48 13 ∗ 2 W 49..61 ( 10 , 7 , 2 , 13 ) 4 ∗ 48 W 1..48 σ 0 4 ∗ 48 W 14..61 σ 1 2 ∗ 2 W 62..63 = 547
对每一轮次:
8 C h 4 M aj 6 Σ 0 6 Σ 1 re d u c e 6 re d u c e 7 = 24
这里第三步总计 24 ∗ 64 = 1792
547 2 ∗ 8 2 3 2
总共是 2099
我们只需要一个有 2 16 3 spread Σ 0..1 σ 0..1 ( 7 , 10 , 11 , 13 , 14 )
行 标签 表格 (16位) spread (32位)
0 0 0000000000000000 00000000000000000000000000000000 1 0 0000000000000001 00000000000000000000000000000001 2 0 0000000000000010 00000000000000000000000000000100 3 0 0000000000000011 00000000000000000000000000000101 ... 0 ... ... 2 7 − 1 0 0000000001111111 00000000000000000001010101010101 2 7 1 0000000010000000 00000000000000000100000000000000 ... 1 ... ... 2 10 − 1 1 0000001111111111 00000000000001010101010101010101 ... 2 ... ... 2 11 − 1 2 0000011111111111 00000000010101010101010101010101 ... 3 ... ... 2 13 − 1 3 0001111111111111 00000001010101010101010101010101 ... 4 ... ... 2 14 − 1 4 0011111111111111 00000101010101010101010101010101 ... 5 ... ... 2 16 − 1 5 1111111111111111 01010101010101010101010101010101
例如,如果要做一次 11 spread 0 , 1 , 2 16 2 1 6
从之前操作来的输入:
E ′ , F ′ , G ′ , E , F , G 64
实际中,我们在分解 E , F , G 16 E ′ , F ′ , G ′
e v e n s spread ( 2 32 − 1 )
e v e n s 0 = e v e n s 1 = spread ( 2 16 − 1 )
s_ch a 0 a 1 a 2 a 3 a 4
0 {0,1,2,3,4,5} P 0 e v e n spread ( P 0 e v e n ) spread ( E l o ) spread ( E hi ) 1 {0,1,2,3,4,5} P 0 o dd spread ( P 0 o dd ) spread ( P 1 o dd ) 0 {0,1,2,3,4,5} P 1 e v e n spread ( P 1 e v e n ) spread ( F l o ) spread ( F hi ) 0 {0,1,2,3,4,5} P 1 o dd spread ( P 1 o dd )
s_ch_neg a 0 a 1 a 2 a 3 a 4 a 5
0 {0,1,2,3,4,5} Q 0 e v e n spread ( Q 0 e v e n ) spread ( E n e g l o ) spread ( E n e g hi ) spread ( E l o ) 1 {0,1,2,3,4,5} Q 0 o dd spread ( Q 0 o dd ) spread ( Q 1 o dd ) spread ( E hi ) 0 {0,1,2,3,4,5} Q 1 e v e n spread ( Q 1 e v e n ) spread ( G l o ) spread ( G hi ) 0 {0,1,2,3,4,5} Q 1 o dd spread ( Q 1 o dd )
约束:
s_ch (choice): L H S − R H S = 0
L H S = a 3 ω − 1 + a 3 ω + 2 32 ( a 4 ω − 1 + a 4 ω ) R H S = a 2 ω − 1 + 2 ∗ a 2 + 2 32 ( a 2 ω + 2 ∗ a 3 )
s_ch_neg (negation): 检查 s_ch 是否为负数在 ( a 0 , a 1 , a 2 ) spread
( a 2 , a 3 )
输出: C h ( E , F , G ) = P o dd + Q o dd = ( P 0 o dd + Q 0 o dd ) + 2 16 ( P 1 o dd + Q 1 o dd )
从之前操作来的输入:
32位字的 A , B , C 64 A ′ , B ′ , C ′ ,
实际中,我们在分解 A , B , C 16 A ′ , B ′ , C ′
s_maj a 0 a 1 a 2 a 3 a 4 a 5
0 {0,1,2,3,4,5} M 0 e v e n spread ( M 0 e v e n ) spread ( A l o ) spread ( A hi ) 1 {0,1,2,3,4,5} M 0 o dd spread ( M 0 o dd ) spread ( M 1 o dd ) spread ( B l o ) spread ( B hi ) 0 {0,1,2,3,4,5} M 1 e v e n spread ( M 1 e v e n ) spread ( C l o ) spread ( C hi ) 0 {0,1,2,3,4,5} M 1 o dd spread ( M 1 o dd )
约束:
s_maj (majority): L H S − R H S = 0
L H S = spread ( M 0 e v e n ) + 2 ⋅ spread ( M 0 o dd ) + 2 32 ⋅ spread ( M 1 e v e n ) + 2 33 ⋅ spread ( M 1 o dd ) R H S = A ′ + B ′ + C ′
在 ( a 0 , a 1 , a 2 ) spread
( a 2 , a 3 )
输出: M aj ( A , B , C ) = M o dd = M 0 o dd + 2 16 M 1 o dd
A ( 2 , 11 , 9 , 10 ) ( a ( 2 ) , b ( 11 ) , c ( 9 ) , d ( 10 )) c ( 9 ) c ( 9 ) l o , c ( 9 ) mi d , c ( 9 ) hi
Σ 0 ( A ) = = ( A ⋙ 2 ) ⊕ ( A ⋙ 13 ) ⊕ ( A ⋙ 22 ) ( A ⋙ 2 ) ⊕ ( A ⋙ 13 ) ⊕ ( A ⋘ 10 )
s_upp_sigma_0 a 0 a 1 a 2 a 3 a 4 a 5 a 6
0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) c ( 9 ) l o spread ( c ( 9 ) l o ) c ( 9 ) mi d spread ( c ( 9 ) mi d ) 1 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( d ( 10 )) spread ( b ( 11 )) c ( 9 ) 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) a ( 2 ) spread ( a ( 2 )) c ( 9 ) hi spread ( c ( 9 ) hi ) 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd )
约束:
s_upp_sigma_0 (Σ 0 L H S − R H S + t a g + d eco m p ose = 0
t a g d eco m p ose L H S = = = co n s t r ai n 1 ( a 0 ω − 1 ) + co n s t r ai n 2 ( a 0 ω ) a ( 2 ) + 2 2 b ( 11 ) + 2 13 c ( 9 ) l o + 2 16 c ( 9 ) mi d + 2 19 c ( 9 ) hi + 2 22 d ( 10 ) − A spread ( R 0 e v e n ) + 2 ⋅ spread ( R 0 o dd ) + 2 32 ⋅ spread ( R 1 e v e n ) + 2 33 ⋅ spread ( R 1 o dd ) R H S = 4 30 spread ( a ( 2 )) 4 21 spread ( b ( 11 )) 4 29 spread ( c ( 9 ) hi ) + + + 4 20 spread ( d ( 10 )) 4 19 spread ( a ( 2 )) 4 26 spread ( c ( 9 ) mi d ) + + + 4 17 spread ( c ( 9 ) hi ) 4 9 spread ( d ( 10 )) 4 23 spread ( c ( 9 ) l o ) + + + 4 14 spread ( c ( 9 ) mi d ) 4 6 spread ( c ( 9 ) hi ) 4 12 spread ( b ( 11 )) + + + 4 11 spread ( c ( 9 ) l o ) 4 3 spread ( c ( 9 ) mi d ) 4 10 spread ( a ( 2 )) + + + spread ( b ( 11 )) spread ( c ( 9 ) l o ) spread ( d ( 10 )) + +
在 a 0 , a 1 , a 2 spread
a ( 2 ) c ( 9 ) l o , c ( 9 ) mi d , c ( 9 ) hi
(见 辅助门 )
输出: Σ 0 ( A ) = R e v e n = R 0 e v e n + 2 16 R 1 e v e n
E ( 6 , 5 , 14 , 7 ) ( a ( 6 ) , b ( 5 ) , c ( 14 ) , d ( 7 )) a ( 6 ) a ( 6 ) l o , a ( 6 ) hi a ( 6 ) l o , a ( 6 ) hi b b ( 5 ) l o , b ( 5 ) hi
Σ 1 ( E ) = = ( E ⋙ 6 ) ⊕ ( E ⋙ 11 ) ⊕ ( E ⋙ 25 ) ( E ⋙ 6 ) ⊕ ( E ⋙ 11 ) ⊕ ( E ⋘ 7 )
s_upp_sigma_1 a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7
0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) b ( 5 ) l o spread ( b ( 5 ) l o ) b ( 5 ) hi spread ( b ( 5 ) hi ) b ( 5 ) 1 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( d ( 7 )) spread ( c ( 14 )) 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) a ( 6 ) l o spread ( a ( 6 ) l o ) a ( 6 ) hi spread ( a ( 6 ) hi ) a ( 6 ) 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd )
约束:
s_upp_sigma_1 (Σ 1 L H S − R H S + t a g + d eco m p ose = 0
t a g d eco m p ose L H S = = = a 0 ω − 1 + co n s t r ai n 4 ( a 0 ω ) a ( 6 ) l o + 2 3 a ( 6 ) hi + 2 6 b ( 5 ) l o + 2 8 b ( 5 ) hi + 2 11 c ( 14 ) + 2 25 d ( 7 ) − E spread ( R 0 e v e n ) + 2 ⋅ spread ( R 0 o dd ) + 2 32 ⋅ spread ( R 1 e v e n ) + 2 33 ⋅ spread ( R 1 o dd ) R H S = 4 29 spread ( a ( 6 ) hi ) 4 29 spread ( b ( 5 ) hi ) 4 18 spread ( c ( 14 )) + + + 4 26 spread ( a ( 6 ) l o ) 4 27 spread ( b ( 5 ) l o ) 4 15 spread ( b ( 5 ) hi ) + + + 4 19 spread ( d ( 7 )) 4 24 spread ( a ( 6 ) hi ) 4 13 spread ( b ( 5 ) l o ) + + + 4 5 spread ( c ( 14 )) 4 21 spread ( a ( 6 ) l o ) 4 10 spread ( a ( 6 ) hi ) + + + 4 2 spread ( b ( 5 ) hi ) 4 14 spread ( d ( 7 )) 4 7 spread ( a ( 6 ) l o ) + + + spread ( b ( 5 ) l o ) spread ( c ( 14 )) spread ( d ( 7 )) + +
在 a 0 , a 1 , a 2 spread
b ( 5 ) l o a ( 6 ) l o , a ( 6 ) hi , b ( 4 ) hi
(见辅助门 )
输出: Σ 1 ( E ) = R e v e n = R 0 e v e n + 2 16 R 1 e v e n
σ 0 ( 3 , 4 , 11 , 14 ) ( a ( 3 ) , b ( 4 ) , c ( 11 ) , d ( 14 )) . b ( 4 ) b ( 4 ) l o , b ( 4 ) hi . spread ( c ( 11 )) spread ( d ( 14 ))
( X ⋙ 7 ) ⊕ ( X ⋙ 18 ) ⊕ ( X ≫ 3 ) ( X ⋙ 7 ) ⊕ ( X ⋘ 14 ) ⊕ ( X ≫ 3 )
s_low_sigma_0 a 0 a 1 a 2 a 3 a 4 a 5 a 6
0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) b ( 4 ) l o spread ( b ( 4 ) l o ) b ( 4 ) hi spread ( b ( 4 ) hi ) 1 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( c ) spread ( d ) b ( 4 ) 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) 0 0 a spread ( a ) 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd )
约束:
s_low_sigma_0 (σ 0 L H S − R H S = 0
L H S = spread ( R 0 e v e n ) + 2 ⋅ spread ( R 0 o dd ) + 2 32 ⋅ spread ( R 1 e v e n ) + 2 33 ⋅ spread ( R 1 o dd ) R H S = 4 30 b ( 4 ) hi 4 21 c ( 11 ) + + 4 15 d ( 14 ) 4 28 b ( 4 ) l o 4 19 b ( 4 ) hi + + + 4 4 c ( 11 ) 4 25 a ( 3 ) 4 17 b ( 4 ) l o + + + 4 2 b ( 4 ) hi 4 11 d ( 14 ) 4 14 a ( 3 ) + + + b ( 4 ) l o c ( 11 ) d ( 14 ) + +
检查 b 是否被正确的分解为4比特位的一些片
b ( 4 ) l o , b ( 4 ) hi a ( 3 )
σ 0 ( 3 , 4 , 3 , 7 , 1 , 1 , 13 ) ( a ( 3 ) , b ( 4 ) , c ( 3 ) , d ( 7 ) , e ( 1 ) , f ( 1 ) , g ( 13 )) . spread ( d ( 7 )) spread ( g ( 13 )) e ( 1 ) , f ( 1 ) b ( 4 ) b ( 4 ) l o , b ( 4 ) hi .
( X ⋙ 7 ) ⊕ ( X ⋙ 18 ) ⊕ ( X ≫ 3 ) ( X ⋙ 7 ) ⊕ ( X ⋘ 14 ) ⊕ ( X ≫ 3 )
s_low_sigma_0_v2 a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7
0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) b ( 4 ) l o spread ( b ( 4 ) l o ) b ( 4 ) hi spread ( b ( 4 ) hi ) 1 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( d ( 7 )) spread ( g ( 13 )) b ( 4 ) e ( 1 ) 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) a ( 3 ) spread ( a ( 3 )) c ( 3 ) spread ( c ( 3 )) f ( 1 ) 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd )
约束:
s_low_sigma_0_v2 (σ 0 L H S − R H S = 0
L H S = spread ( R 0 e v e n ) + 2 ⋅ spread ( R 0 o dd ) + 2 32 ⋅ spread ( R 1 e v e n ) + 2 33 ⋅ spread ( R 1 o dd ) R H S = 4 30 b ( 4 ) hi 4 31 e ( 1 ) + + 4 16 g ( 13 ) 4 28 b ( 4 ) l o 4 24 d ( 7 ) + + + 4 15 f ( 1 ) 4 25 a ( 3 ) 4 21 c ( 3 ) + + + 4 14 e ( 1 ) 4 12 g ( 13 ) 4 19 b ( 4 ) hi + + + 4 7 d ( 7 ) 4 11 f ( 1 ) 4 17 b ( 4 ) l o + + + 4 4 c ( 3 ) 4 10 e ( 1 ) 4 14 a ( 3 ) + + + 4 2 b ( 4 ) hi 4 3 d ( 7 ) 4 1 g ( 13 ) + + + b ( 4 ) l o c ( 3 ) f ( 1 ) + +
检查 b 是否被正确的分解为4比特位的片
b ( 4 ) l o , b ( 4 ) hi a ( 3 ) , c ( 3 )
σ 1 ( 10 , 7 , 2 , 13 ) ( a ( 10 ) , b ( 7 ) , c ( 2 ) , d ( 13 )) . b ( 7 ) ( 2 , 2 , 3 ) b ( 7 ) l o , b ( 7 ) mi d , b ( 7 ) hi . spread ( a ( 10 )) spread ( d ( 13 ))
( X ⋙ 17 ) ⊕ ( X ⋙ 19 ) ⊕ ( X ≫ 10 ) ( X ⋘ 15 ) ⊕ ( X ⋘ 13 ) ⊕ ( X ≫ 10 )
s_low_sigma_1 a 0 a 1 a 2 a 3 a 4 a 5 a 6
0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) b ( 7 ) l o spread ( b ( 7 ) l o ) b ( 7 ) mi d spread ( b ( 7 ) mi d ) 1 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( a ( 10 )) spread ( d ( 13 )) b ( 7 ) 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) c ( 2 ) spread ( c ( 2 )) b ( 7 ) hi spread ( b ( 7 ) hi ) 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd )
约束:
s_low_sigma_1 (σ 1 L H S − R H S = 0 L H S = spread ( R 0 e v e n ) + 2 ⋅ spread ( R 0 o dd ) + 2 32 ⋅ spread ( R 1 e v e n ) + 2 33 ⋅ spread ( R 1 o dd ) R H S = 4 29 b ( 7 ) hi 4 30 c ( 2 ) + + 4 9 d ( 13 ) 4 27 b ( 7 ) mi d 4 27 b ( 7 ) hi + + + 4 7 c ( 2 ) 4 25 b ( 7 ) l o 4 25 b ( 7 ) mi d + + + 4 4 b ( 7 ) hi 4 15 a ( 10 ) 4 23 b ( 7 ) l o + + + 4 2 b ( 7 ) mi d 4 2 d ( 13 ) 4 13 a ( 10 ) + + + b ( 7 ) l o c ( 2 ) d ( 13 ) + +
检查 b 是否被正确的分解为7比特位的片。
W b ( 7 ) l o + 2 2 W b ( 7 ) mi d + 2 4 W b ( 7 ) hi − W = 0
b ( 7 ) l o , b ( 7 ) mi d , c ( 2 )
b ( 7 ) hi
σ 1 ( 3 , 4 , 3 , 7 , 1 , 1 , 13 ) ( a ( 3 ) , b ( 4 ) , c ( 3 ) , d ( 7 ) , e ( 1 ) , f ( 1 ) , g ( 13 )) . spread ( d ( 7 )) spread ( g ( 13 )) e ( 1 ) , f ( 1 ) b ( 4 ) b ( 4 ) l o , b ( 4 ) hi .
( X ⋙ 17 ) ⊕ ( X ⋙ 19 ) ⊕ ( X ≫ 10 ) ( X ⋘ 15 ) ⊕ ( X ⋘ 13 ) ⊕ ( X ≫ 10 )
s_low_sigma_1_v2 a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7
0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) b ( 4 ) l o spread ( b ( 4 ) l o ) b ( 4 ) hi spread ( b ( 4 ) hi ) 1 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( d ( 7 )) spread ( g ( 13 )) b ( 4 ) e ( 1 ) 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) a ( 3 ) spread ( a ( 3 )) c ( 3 ) spread ( c ( 3 )) f ( 1 ) 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd )
约束:
s_low_sigma_1_v2 (σ 1 L H S − R H S = 0
L H S = spread ( R 0 e v e n ) + 2 ⋅ spread ( R 0 o dd ) + 2 32 ⋅ spread ( R 1 e v e n ) + 2 33 ⋅ spread ( R 1 o dd ) R H S = 4 25 d ( 7 ) 4 31 f ( 1 ) + + 4 22 c ( 3 ) 4 30 e ( 1 ) + + 4 20 b ( 4 ) hi 4 23 d ( 7 ) + + 4 9 g ( 13 ) 4 18 b ( 4 ) l o 4 20 c ( 3 ) + + + 4 8 f ( 1 ) 4 15 a 4 18 b ( 4 ) hi + + + 4 7 e ( 1 ) 4 2 g ( 13 ) 4 16 b ( 4 ) l o + + + d ( 7 ) 4 1 f ( 1 ) 4 13 a + + + e ( 1 ) g ( 13 ) +
检查 b 是否被正确的分解为4比特位的子片。
b ( 4 ) l o , b ( 4 ) hi a ( 3 ) , c ( 3 )
令 co n s t r ai n n ( x ) = ∏ i = 0 n ( x − i ) x ∈ [ 0.. n ] .
( a − 3 ) ( a − 2 ) ( a − 1 ) ( a ) = 0
l 1 ( a ) + 4 ∗ l 2 ( a ) + 5 ∗ l 3 ( a ) − a ′ = 0
插值多项式:
l 0 ( a ) = ( − 3 ) ( − 2 ) ( − 1 ) ( a − 3 ) ( a − 2 ) ( a − 1 ) spread ( 00 ) = 0000 l 1 ( a ) = ( − 2 ) ( − 1 ) ( 1 ) ( a − 3 ) ( a − 2 ) ( a ) spread ( 01 ) = 0001 l 2 ( a ) = ( − 1 ) ( 1 ) ( 2 ) ( a − 3 ) ( a − 1 ) ( a ) spread ( 10 ) = 0100 l 3 ( a ) = ( 1 ) ( 2 ) ( 3 ) ( a − 2 ) ( a − 1 ) ( a ) spread ( 11 ) = 0101
( a − 7 ) ( a − 6 ) ( a − 5 ) ( a − 4 ) ( a − 3 ) ( a − 2 ) ( a − 1 ) ( a ) = 0
l 1 ( a ) + 4 ∗ l 2 ( a ) + 5 ∗ l 3 ( a ) + 16 ∗ l 4 ( a ) + 17 ∗ l 5 ( a ) + 20 ∗ l 6 ( a ) + 21 ∗ l 7 ( a ) − a ′ = 0
插值多项式:
l 0 ( a ) = ( − 7 ) ( − 6 ) ( − 5 ) ( − 4 ) ( − 3 ) ( − 2 ) ( − 1 ) ( a − 7 ) ( a − 6 ) ( a − 5 ) ( a − 4 ) ( a − 3 ) ( a − 2 ) ( a − 1 ) spread ( 000 ) = 000000 l 1 ( a ) = ( − 6 ) ( − 5 ) ( − 4 ) ( − 3 ) ( − 2 ) ( − 1 ) ( 1 ) ( a − 7 ) ( a − 6 ) ( a − 5 ) ( a − 4 ) ( a − 3 ) ( a − 2 ) ( a ) spread ( 001 ) = 000001 l 2 ( a ) = ( − 5 ) ( − 4 ) ( − 3 ) ( − 2 ) ( − 1 ) ( 1 ) ( 2 ) ( a − 7 ) ( a − 6 ) ( a − 5 ) ( a − 4 ) ( a − 3 ) ( a − 1 ) ( a ) spread ( 010 ) = 000100 l 3 ( a ) = ( − 4 ) ( − 3 ) ( − 2 ) ( − 1 ) ( 1 ) ( 2 ) ( 3 ) ( a − 7 ) ( a − 6 ) ( a − 5 ) ( a − 3 ) ( a − 2 ) ( a − 1 ) ( a ) spread ( 011 ) = 000101 l 4 ( a ) = ( − 3 ) ( − 2 ) ( − 1 ) ( 1 ) ( 2 ) ( 3 ) ( 4 ) ( a − 7 ) ( a − 6 ) ( a − 5 ) ( a − 3 ) ( a − 2 ) ( a − 1 ) ( a ) spread ( 100 ) = 010000 l 5 ( a ) = ( − 2 ) ( − 1 ) ( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 5 ) ( a − 7 ) ( a − 6 ) ( a − 4 ) ( a − 3 ) ( a − 2 ) ( a − 1 ) ( a ) spread ( 101 ) = 010001 l 6 ( a ) = ( − 1 ) ( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 5 ) ( 6 ) ( a − 7 ) ( a − 5 ) ( a − 4 ) ( a − 3 ) ( a − 2 ) ( a − 1 ) ( a ) spread ( 110 ) = 010100 l 7 ( a ) = ( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 5 ) ( 6 ) ( 7 ) ( a − 6 ) ( a − 5 ) ( a − 4 ) ( a − 3 ) ( a − 2 ) ( a − 1 ) ( a ) spread ( 111 ) = 010101
6元素的 ( mod 2 32 )
输入:
E { e i l o , e i hi } i = 0 5 c a rry
检查: E = e 0 + e 1 + e 2 + e 3 + e 4 + e 5 ( mod 32 )
假设输入被约束为16个比特位
加法门 (sa):
a 0 + a 1 + a 2 + a 3 + a 4 + a 5 + a 6 − a 7 = 0
进位门 (sc):
2 16 a 6 ω − 1 + a 6 + [( a 6 − 5 ) ( a 6 − 4 ) ( a 6 − 3 ) ( a 6 − 2 ) ( a 6 − 1 ) ( a 6 )] = 0
sa sc a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7
1 0 e 0 l o e 1 l o e 2 l o e 3 l o e 4 l o e 5 l o − c a rry ∗ 2 16 E l o 1 1 e 0 hi e 1 hi e 2 hi e 3 hi e 4 hi e 5 hi c a rry E hi
假设输入被约束为16个比特位
加法门 (sa):
a 0 ω − 1 + a 1 ω − 1 + a 2 ω − 1 + a 0 + a 1 + a 2 + a 3 ω − 1 − a 3 = 0
进位门 (sc):
sa sc a 0 a 1 a 2 a 3
0 0 e 0 l o e 1 l o e 2 l o − c a rry ∗ 2 16 1 1 e 3 l o e 4 l o e 5 l o E l o 0 0 e 0 hi e 1 hi e 2 hi c a rry 1 0 e 3 hi e 4 hi e 5 hi E hi
7元素的 ( mod 2 32 )
输入:
E { e i l o , e i hi } i = 0 6 c a rry
检查: E = e 0 + e 1 + e 2 + e 3 + e 4 + e 5 + e 6 ( mod 32 )
假设输入被约束为16个比特位
加法门 (sa):
a 0 + a 1 + a 2 + a 3 + a 4 + a 5 + a 6 + a 7 − a 8 = 0
进位门 (sc):
2 16 a 7 ω − 1 + a 7 + [( a 7 − 6 ) ( a 7 − 5 ) ( a 7 − 4 ) ( a 7 − 3 ) ( a 7 − 2 ) ( a 7 − 1 ) ( a 7 )] = 0
sa sc a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8
1 0 e 0 l o e 1 l o e 2 l o e 3 l o e 4 l o e 5 l o e 6 l o − c a rry ∗ 2 16 E l o 1 1 e 0 hi e 1 hi e 2 hi e 3 hi e 4 hi e 5 hi e 6 hi c a rry E hi
对于消息 M ∈ { 0 , 1 } 512
通过将 M M = W 0 ∣∣ W 1 ∣∣ ⋯ ∣∣ W 14 ∣∣ W 15 ;
剩下的48个字使用如下的方式构造:
W i = σ 1 ( W i − 2 ) ⊞ W i − 7 ⊞ σ 0 ( W i − 15 ) ⊞ W i − 16 , 16 ≤ i < 64
sw sd0 sd1 sd2 sd3 ss0 ss0_v2 ss1 ss1_v2 a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9
0 1 0 0 0 0 0 0 0 {0,1,2,3,4,5} W 0 l o spread ( W 0 l o ) W 0 l o W 0 hi W 0 σ 0 ( W 1 ) l o σ 1 ( W 14 ) l o W 9 l o 1 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} W 0 hi spread ( W 0 hi ) W 16 σ 0 ( W 1 ) hi σ 1 ( W 14 ) hi W 9 hi c a rr y 16 0 1 1 0 0 0 0 0 0 {0,1,2,3,4} W 1 d ( 14 ) spread ( W 1 d ( 14 ) ) W 1 l o W 1 hi W 1 σ 0 ( W 2 ) l o σ 1 ( W 15 ) l o W 10 l o 1 0 0 0 0 0 0 0 0 {0,1,2} W 1 c ( 11 ) spread ( W 1 c ( 11 ) ) W 1 a ( 3 ) W 1 b ( 4 ) W 17 σ 0 ( W 2 ) hi σ 1 ( W 15 ) hi W 10 hi c a rr y 17 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) W 1 b ( 4 ) l o spread ( W 1 b ( 4 ) l o ) W 1 b ( 4 ) hi spread ( W 1 b ( 4 ) hi ) 0 0 0 0 0 1 0 0 0 {0,1,2,3,4,5} R 1 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( W 1 c ( 11 ) ) spread ( W 1 d ( 14 ) ) W 1 b ( 4 ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 o dd spread ( R 1 e v e n ) 0 0 W 1 a ( 3 ) spread ( W 1 a ( 3 ) ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 o dd ) σ 0 v 1 R 0 σ 0 v 1 R 1 σ 0 v 1 R 0 e v e n σ 0 v 1 R 0 o dd .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 0 0 0 0 0 0 0 0 0 {0,1,2,3} W 14 g ( 13 ) spread ( W 14 g ( 13 ) ) W 14 a ( 3 ) W 14 c ( 3 ) 0 1 0 1 0 0 0 0 0 0 W 14 d ( 7 ) spread ( W 14 d ( 7 ) ) W 14 l o W 14 hi W 14 σ 0 ( W 15 ) l o σ 1 ( W 28 ) l o W 23 l o 1 0 0 0 0 0 0 0 0 0 W 14 b ( 4 ) spread ( W 14 b ( 4 ) ) W 14 e ( 1 ) W 14 f ( 1 ) W 30 σ 0 ( W 15 ) hi σ 1 ( W 28 ) hi W 23 hi c a rr y 30 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) W 14 b ( 4 ) l o spread ( W 14 b ( 4 ) l o ) W 14 b ( 4 ) hi spread ( W 14 b ( 4 ) hi ) 0 0 0 0 0 0 1 0 0 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( W 14 d ( 7 ) ) spread ( W 14 g ( 13 ) ) W 1 b ( 14 ) W 14 e ( 1 ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) W 14 a ( 3 ) spread ( W 14 a ( 3 ) ) W 14 c ( 3 ) spread ( W 14 c ( 3 ) ) W 14 f ( 1 ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd ) σ 0 v 2 R 0 σ 0 v 2 R 1 σ 0 v 2 R 0 e v e n σ 0 v 2 R 0 o dd 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) W 14 b ( 4 ) l o spread ( W 14 b ( 4 ) l o ) W 14 b ( 4 ) hi spread ( W 14 b ( 4 ) hi ) 0 0 0 0 0 0 0 0 1 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( d ) spread ( g ) W 14 e ( 1 ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) W 14 a ( 3 ) spread ( W 14 a ( 3 ) ) W 14 c ( 3 ) spread ( W 14 c ( 3 ) ) W 14 f ( 1 ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd ) σ 1 v 2 R 0 σ 1 v 2 R 1 σ 1 v 2 R 0 e v e n σ 1 v 2 R 0 o dd .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 0 1 0 0 1 0 0 0 0 {0,1,2,3} W 49 d ( 13 ) spread ( W 49 d ( 13 ) ) W 49 l o W 49 hi W 49 0 0 0 0 0 0 0 0 0 {0,1} W 49 a ( 10 ) spread ( W 49 a ( 10 ) ) W 49 c ( 2 ) W 49 b ( 7 ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) W 49 b ( 7 ) l o spread ( W 49 b ( 7 ) l o ) W 49 b ( 7 ) mi d spread ( W 49 b ( 7 ) mi d ) 0 0 0 0 0 0 0 0 1 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( a ) spread ( d ) W 1 b ( 49 ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) W 49 c ( 2 ) spread ( W 49 c ( 2 ) ) W 49 b ( 7 ) hi spread ( W 49 b ( 7 ) hi ) 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd ) σ 1 v 1 R 0 σ 1 v 1 R 1 σ 1 v 1 R 0 e v e n σ 1 v 1 R 0 o dd .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 0 1 0 0 0 0 0 0 0 {0,1,2,3,4,5} W 62 l o spread ( W 62 l o ) W 62 l o W 62 hi W 62 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} W 62 hi spread ( W 62 hi ) 0 1 0 0 0 0 0 0 0 {0,1,2,3,4,5} W 63 l o spread ( W 63 l o ) W 63 l o W 63 hi W 63 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} W 63 hi spread ( W 63 hi )
约束:
sw: 使用 re d u c e 4 sd0: W 0 , W 62 , W 63 sd1: W 1..13 ( 3 , 4 , 11 , 14 )
W a ( 3 ) + 2 3 W b ( 4 ) l o + 2 5 W b ( 4 ) hi + 2 7 W c ( 11 ) + 2 18 W d ( 14 ) − W = 0
sd2: W 14..48 ( 3 , 4 , 3 , 7 , 1 , 1 , 13 )
W a ( 3 ) + 2 3 W b ( 4 ) l o + 2 5 W b ( 4 ) hi + 2 7 W c ( 11 ) + 2 10 W d ( 14 ) + 2 17 W e ( 1 ) + 2 18 W f ( 1 ) + 2 19 W g ( 13 ) − W = 0
sd3: W 49..61 ( 10 , 7 , 2 , 13 )
W a ( 10 ) + 2 10 W b ( 7 ) l o + 2 12 W b ( 7 ) mi d + 2 15 W b ( 7 ) hi + 2 17 W c ( 2 ) + 2 19 W d ( 13 ) − W = 0
+----------------------------------------------------------+
| |
| 分解 E, |
| Σ_1(E) |
| |
| +---------------------------------------+
| | |
| | reduce_5() 以获得 H' |
| | |
+----------------------------------------------------------+
| 分解 F, 分解 G |
| |
| Ch(E,F,G) |
| |
+----------------------------------------------------------+
| |
| 分解 A, |
| Σ_0(A) |
| |
| |
| +---------------------------------------+
| | |
| | 使用 H' 和 reduce_7(), |
| | 以获得 A_new |
| | |
+------------------+---------------------------------------+
| 分解 B, 分解 C |
| |
| Maj(A,B,C) |
| |
| +---------------------------------------+
| | 使用 H' 和 reduce_6(), |
| | 以获得 E_new |
| | |
+------------------+---------------------------------------+
s_digest sd_abcd sd_efgh ss0 ss1 s_maj s_ch_neg s_ch s_a_new s_e_new s_h_prime a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9
0 0 1 0 0 0 0 0 0 0 0 {0,1,2} F 0 d ( 7 ) spread ( E 0 d ( 7 )) E 0 b ( 5 ) l o spread ( E 0 b ( 5 ) l o ) E 0 b ( 5 ) hi spread ( E 0 b ( 5 ) hi ) E 0 l o spread ( E 0 l o ) 0 0 0 0 0 0 0 0 0 0 0 {0,1} E 0 c ( 14 ) spread ( E 0 c ( 14 )) E 0 a ( 6 ) l o spread ( E 0 a ( 6 ) l o ) E 0 a ( 6 ) hi spread ( E 0 a ( 6 ) hi ) E 0 hi spread ( E 0 hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) spread ( E 0 b ( 5 ) l o ) spread ( E 0 b ( 5 ) hi ) 0 0 0 0 1 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( E 0 d ( 7 )) spread ( E 0 c ( 14 )) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) spread ( E 0 a ( 6 ) l o ) spread ( E 0 a ( 6 ) hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd ) 0 0 1 0 0 0 0 0 0 0 0 {0,1,2} F 0 d ( 7 ) spread ( F 0 d ( 7 )) F 0 b ( 5 ) l o spread ( F 0 b ( 5 ) l o ) F 0 b ( 5 ) hi spread ( F 0 b ( 5 ) hi ) F 0 l o spread ( F 0 l o ) 0 0 0 0 0 0 0 0 0 0 0 {0,1} F 0 c ( 14 ) spread ( F 0 c ( 14 )) F 0 a ( 6 ) l o spread ( F 0 a ( 6 ) l o ) F 0 a ( 6 ) hi spread ( F 0 a ( 6 ) hi ) F 0 hi spread ( F 0 hi ) 0 0 1 0 0 0 0 0 0 0 0 {0,1,2} G 0 d ( 7 ) spread ( G 0 d ( 7 )) G 0 b ( 5 ) l o spread ( G 0 b ( 5 ) l o ) G 0 b ( 5 ) hi spread ( G 0 b ( 5 ) hi ) G 0 l o spread ( G 0 l o ) 0 0 0 0 0 0 0 0 0 0 0 {0,1} G 0 c ( 14 ) spread ( G 0 c ( 14 )) G 0 a ( 6 ) l o spread ( G 0 a ( 6 ) l o ) G 0 a ( 6 ) hi spread ( G 0 a ( 6 ) hi ) G 0 hi spread ( G 0 hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} P 0 e v e n spread ( P 0 e v e n ) spread ( E l o ) spread ( E hi ) Q 0 o dd K 0 l o H 0 l o W 0 l o 0 0 0 0 0 0 0 1 0 0 1 {0,1,2,3,4,5} P 0 o dd spread ( P 0 o dd ) spread ( P 1 o dd ) Σ 1 ( E 0 ) l o Σ 1 ( E 0 ) hi K 0 hi H 0 hi W 0 hi 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} P 1 e v e n spread ( P 1 e v e n ) spread ( F l o ) spread ( F hi ) Q 1 o dd P 1 o dd H p r im e 0 l o H p r im e 0 hi H p r im e 0 c a rry 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} P 1 o dd spread ( P 1 o dd ) D 0 l o E 1 l o 0 0 0 0 0 0 0 0 0 1 0 {0,1,2,3,4,5} Q 0 e v e n spread ( Q 0 e v e n ) spread ( E n e g l o ) spread ( E n e g hi ) spread ( E l o ) D 0 hi E 1 hi E 1 c a rry 0 0 0 0 0 0 1 0 0 0 0 {0,1,2,3,4,5} Q 0 o dd spread ( Q 0 o dd ) spread ( Q 1 o dd ) spread ( E hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} Q 1 e v e n spread ( Q 1 e v e n ) spread ( G l o ) spread ( G hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} Q 1 o dd spread ( Q 1 o dd ) 0 1 0 0 0 0 0 0 0 0 0 {0,1,2} A 0 b ( 11 ) spread ( A 0 b ( 11 )) A 0 c ( 9 ) l o spread ( A 0 c ( 9 ) l o ) A 0 c ( 9 ) mi d spread ( A 0 c ( 9 ) mi d ) A 0 l o spread ( A 0 l o ) 0 0 0 0 0 0 0 0 0 0 0 {0,1} A 0 d ( 10 ) spread ( A 0 d ( 10 )) A 0 a ( 2 ) spread ( A 0 a ( 2 )) A 0 c ( 9 ) hi spread ( A 0 c ( 9 ) hi ) A 0 hi spread ( A 0 hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) spread ( c ( 9 ) l o ) spread ( c ( 9 ) mi d ) 0 0 0 1 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( d ( 10 )) spread ( b ( 11 )) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) spread ( a ( 2 )) spread ( c ( 9 ) hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd ) 0 1 0 0 0 0 0 0 0 0 0 {0,1,2} B 0 b ( 11 ) spread ( B 0 b ( 11 )) B 0 c ( 9 ) l o spread ( B 0 c ( 9 ) l o ) B 0 c ( 9 ) mi d spread ( B 0 c ( 9 ) mi d ) B 0 l o spread ( B 0 l o ) 0 0 0 0 0 0 0 0 0 0 0 {0,1} B 0 d ( 10 ) spread ( B 0 d ( 10 )) B 0 a ( 2 ) spread ( B 0 a ( 2 )) B 0 c ( 9 ) hi spread ( B 0 c ( 9 ) hi ) B 0 hi spread ( B 0 hi ) 0 1 0 0 0 0 0 0 0 0 0 {0,1,2} C 0 b ( 11 ) spread ( C 0 b ( 11 )) C 0 c ( 9 ) l o spread ( C 0 c ( 9 ) l o ) C 0 c ( 9 ) mi d spread ( C 0 c ( 9 ) mi d ) C 0 l o spread ( C 0 l o ) 0 0 0 0 0 0 0 0 0 0 0 {0,1} C 0 d ( 10 ) spread ( C 0 d ( 10 )) C 0 a ( 2 ) spread ( C 0 a ( 2 )) C 0 c ( 9 ) hi spread ( C 0 c ( 9 ) hi ) C 0 hi spread ( C 0 hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} M 0 e v e n spread ( M 0 e v e n ) M 1 o dd spread ( A 0 l o ) spread ( A 0 hi ) H p r im e 0 l o H p r im e 0 hi 0 0 0 0 0 1 0 0 1 0 0 {0,1,2,3,4,5} M 0 o dd spread ( M 0 o dd ) spread ( M 1 o dd ) spread ( B 0 l o ) spread ( B 0 hi ) Σ 0 ( A 0 ) l o A 1 l o A 1 c a rry 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} M 1 e v e n spread ( M 1 e v e n ) spread ( C 0 l o ) spread ( C 0 hi ) Σ 0 ( A 0 ) hi A 1 hi 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} M 1 o dd spread ( M 1 o dd )
s_digest sd_abcd sd_efgh ss0 ss1 s_maj s_ch_neg s_ch s_a_new s_e_new s_h_prime a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9
0 0 1 0 0 0 0 0 0 0 0 {0,1,2} F 0 d ( 7 ) spread ( E 0 d ( 7 )) E 0 b ( 5 ) l o spread ( E 0 b ( 5 ) l o ) E 0 b ( 5 ) hi spread ( E 0 b ( 5 ) hi ) E 0 l o spread ( E 0 l o ) 0 0 0 0 0 0 0 0 0 0 0 {0,1} E 0 c ( 14 ) spread ( E 0 c ( 14 )) E 0 a ( 6 ) l o spread ( E 0 a ( 6 ) l o ) E 0 a ( 6 ) hi spread ( E 0 a ( 6 ) hi ) E 0 hi spread ( E 0 hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) spread ( E 0 b ( 5 ) l o ) spread ( E 0 b ( 5 ) hi ) 0 0 0 0 1 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( E 0 d ( 7 )) spread ( E 0 c ( 14 )) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) spread ( E 0 a ( 6 ) l o ) spread ( E 0 a ( 6 ) hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} P 0 e v e n spread ( P 0 e v e n ) spread ( E l o ) spread ( E hi ) Q 0 o dd K 0 l o H 0 l o W 0 l o 0 0 0 0 0 0 0 1 0 0 1 {0,1,2,3,4,5} P 0 o dd spread ( P 0 o dd ) spread ( P 1 o dd ) Σ 1 ( E 0 ) l o Σ 1 ( E 0 ) hi K 0 hi H 0 hi W 0 hi 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} P 1 e v e n spread ( P 1 e v e n ) spread ( F l o ) spread ( F hi ) Q 1 o dd P 1 o dd H p r im e 0 l o H p r im e 0 hi H p r im e 0 c a rry 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} P 1 o dd spread ( P 1 o dd ) D 0 l o E 1 l o 0 0 0 0 0 0 0 0 0 1 0 {0,1,2,3,4,5} Q 0 e v e n spread ( Q 0 e v e n ) spread ( E n e g l o ) spread ( E n e g hi ) spread ( E l o ) D 0 hi E 1 hi E 1 c a rry 0 0 0 0 0 0 1 0 0 0 0 {0,1,2,3,4,5} Q 0 o dd spread ( Q 0 o dd ) spread ( Q 1 o dd ) spread ( E hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} Q 1 e v e n spread ( Q 1 e v e n ) spread ( G l o ) spread ( G hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} Q 1 o dd spread ( Q 1 o dd ) 0 1 0 0 0 0 0 0 0 0 0 {0,1,2} A 0 b ( 11 ) spread ( A 0 b ( 11 )) A 0 c ( 9 ) l o spread ( A 0 c ( 9 ) l o ) A 0 c ( 9 ) mi d spread ( A 0 c ( 9 ) mi d ) A 0 l o spread ( A 0 l o ) 0 0 0 0 0 0 0 0 0 0 0 {0,1} A 0 d ( 10 ) spread ( A 0 d ( 10 )) A 0 a ( 2 ) spread ( A 0 a ( 2 )) A 0 c ( 9 ) hi spread ( A 0 c ( 9 ) hi ) A 0 hi spread ( A 0 hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 e v e n spread ( R 0 e v e n ) spread ( c ( 9 ) l o ) spread ( c ( 9 ) mi d ) 0 0 0 1 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 0 o dd spread ( R 0 o dd ) spread ( R 1 o dd ) spread ( d ( 10 )) spread ( b ( 11 )) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 e v e n spread ( R 1 e v e n ) spread ( a ( 2 )) spread ( c ( 9 ) hi ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} R 1 o dd spread ( R 1 o dd ) 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} M 0 e v e n spread ( M 0 e v e n ) M 1 o dd spread ( A 0 l o ) spread ( A 0 hi ) H p r im e 0 l o H p r im e 0 hi 0 0 0 0 0 1 0 0 1 0 0 {0,1,2,3,4,5} M 0 o dd spread ( M 0 o dd ) spread ( M 1 o dd ) spread ( B 0 l o ) spread ( B 0 hi ) Σ 0 ( A 0 ) l o A 1 l o A 1 c a rry 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} M 1 e v e n spread ( M 1 e v e n ) spread ( C 0 l o ) spread ( C 0 hi ) Σ 0 ( A 0 ) hi A 1 hi 0 0 0 0 0 0 0 0 0 0 0 {0,1,2,3,4,5} M 1 o dd spread ( M 1 o dd )
s_digest sd_abcd sd_efgh ss0 ss1 s_maj s_ch_neg s_ch s_a_new s_e_new s_h_prime a 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9
1 0 0 0 0 0 0 0 0 0 0 0 0 0 A 63 l o A 63 hi A 63 B 63 l o B 63 hi B 63 0 0 0 0 0 0 0 0 0 0 0 0 0 0 C 63 l o C 63 hi C 63 C 63 l o C 63 hi C 63 1 0 0 0 0 0 0 0 0 0 0 0 0 0 E 63 l o E 63 hi E 63 G 63 l o G 63 hi G 63 0 0 0 0 0 0 0 0 0 0 0 0 0 0 F 63 l o F 63 hi F 63 H 63 l o H 63 hi H 63