halo2 
重要提示: 这个库正在积极开发中,不应该在生产软件中使用.
文档
最低支持的 Rust 版本
需要 Rust 1.51 或者更高.
最低支持的 rust 版本 可以在 未来更改, 但是这会带来小版本的改变
并行控制方案
halo2 当前为并行计算使用 rayon .
设置 线程数量数量时使用 RAYON_NUM_THREADS 环境变量
许可证
Copyright 2020-2021 The Electric Coin Company.
你可以在 Bootstrap 开源许可证 1.0 版下使用这个包,
或者您可以选择任意更高版本 . 看这个文件 COPYING 去了解更多详细信息,
看这个文件 LICENSE-BOSL 了解 Bootstrap 开源许可证 1.0 版条款.
BOSL的目的是允许对包进行商业改进,同时确保所有改进都是开源的 . 看 这 去了解 BOSL 为什么存在.
翻译说明
Thanks for halo2 Book team's clear explanation about halo2 design and protocol. It's really wonderful :)
halo2 Book清晰系统地讲解了halo2零知识证明的原理:电路算术表示,查找证明,置换证明以及整个协议的形式化表示。同时该文档也讲解零知识证明基础原理,是入门PLONK系零知识证明的极佳入门材料。
在查看halo2实现代码的基础上,对照halo2 Book设计,总结出halo2 Book对应的中文翻译。国内零知识证明技术相关的正规教程/教材比较少,有些术语并没有合适或者统一的翻译。针对用到的术语,整理了一个术语表。有些术语实在无法精准翻译,直接用英文代替。此翻译对应的halo2 Book的最后一个提交信息如下:
658c2db4217b1b19b17ecd29577c0e370e1c4997
halo2 Book的翻译以严格准守原文本意为原则,但是水平有限,有翻译不妥的地方,欢迎更多的小伙伴指正。最后感谢参与翻译和校对的小伙伴们。
Github: Halo2 Book (Chinese)
术语表
-
PLONKish: PLONK系
-
argument: 证明
-
language: 语言
-
relation: 关系
-
statement: 论述
-
witness: 论据
-
soundness: 可靠性
-
circuit: 电路
-
public input: 公开输入
-
private input: 隐私输入
-
arithmetization:算术化
-
custom gate: 自定义门
-
lookup: 查找表
-
field:域
-
grand product: 大乘积
-
generalization: 泛化
-
selector: 选择子
-
row: 行
-
column: 列
-
cell:单元格
-
lagrange basis polynomial: 拉格朗日基多项式
-
floor planner:布局器
-
gadget:小工具
-
scalar: 标量
-
vanishing polynomial:消退多项式
相关概念
首先,我们将描述零知识证明系统halo2依赖的算术化(电路描述方法); 其次介绍电路实现的相关抽象概念。
证明系统
证明系统 的目标是能够证明有趣的数学或者密码学论述.
通常,在一个给定的协议中,我们想要证明不同公共输入的一系列论述。证明者需要展示他们知道一些隐私输入,满足论述。
为此,我们描绘了一个关系,,这个关系指定哪些公共输入和隐私输入组合是有效的。
上面的术语和 ZKProof Community Reference 保持一致
准确地说,我们应该区分关系 和它在证明系统中实现。后者我们称为电路。
我们用来表示特定证明系统的电路的语言叫做算术化。通常,算术化会以多项式约束的形式定义电路。这些约束作用于某个域上的变量。
将一个特定关系的表达成电路的过程有时也叫作 "算术化", 但是我们避免这种叫法。
为了生成一个论述的证明, 证明者需要知道电路需要的隐私输入以及中间值,这些称为advice。
我们假设我们能通过隐私和公开输入计算出advice。这些advice值依赖于我们实现的电路,而不仅仅取决于论述。
隐私输入和advice一起称为论据( witness)。
有些作者将隐私输入看成论据, 但是在我们看来, 论据还包括advice,即论据包括证明者提供给电路的所有值。
举个例子, 假设我们想证明原像 经过哈希函数 得到摘要 :
-
原像 是隐私输入
-
摘要是公开输入
-
关系为 .
-
对于特定的公共输入 , 论述是.
-
advice是实现哈希函数的电路中的所有中间值。论据是和advice。
非交互式证明允许证明者对特定的论述和论据生成一个证明。证明可以使验证者相信存在论据使论述成立。这种证明不能错误地说服验证者的安全特性称为可靠性。
非交互式知识证明(NARK)进一步使验证者确信证明者知道使论述成立的论据。这个安全属性称为知识可靠性,它暗示了可靠性。
在实践中,对于密码协议来说,知识可靠性比可靠性更有用:如果我们对在某个协议中Alice是否持有密钥感兴趣,我们需要Alice证明她知道密钥,而不仅仅是密钥存在。
知识的可靠性是通过一个提取器来证明。提取器精确观察证明生成过程,能计算出论据。
如果证明是可塑的,这个性质有点微妙。 也就是说,有些证明系统,在不知道论据的情况下,在现有证明的基础上修改生成新的证明。使用了可塑证明系统的协议需要考虑这一点。
即使没有可塑性, 证明也很可能回放。举个例子,在我们的例子中,我们不希望Alice能够提交别人生成的证明,证明她知道密钥。
如果一个证明没有论据相关信息(除了论据信息存在和证明者知道这些信息外), 我们说这样的证明系统是零知识的。
如果证明系统能生成简短的证明 - 相对电路大小多项式对数大小的话,我们说,证明是简洁的。 一个简洁的NARK叫做 snark(简洁的非交互式证明 - Succinct Non-Interactive Argument of Knowledge)。
根据这个定义, 一个SNARK不需要关于电路大小的多项式对数级验证时间。有些论文使用术语有效性(efficient)来描述具有这种性质的SNARK,但我们将避免使用这个术语,因为它对于支持聚合或递归验证的SNARK来说,语义是模糊的,我们稍后会讲。
zk-SNARK 叫做零知识SNARK。
PLONK化算术化
halo2采用的算术化来自于 PLONK,或者更准确地说,来自它的扩展UltraPLONK,支持自定义门和查找表。我们称之为PLONK化( PLONKish)。
PLONK化电路是用矩形矩阵定义的。矩阵的行,列,单元格 和传统矩阵叫法意义一致。
PLONK化电路依赖配置 (configuation):
-
一个有限域,其中单元格的值(给定论述和论据)是的元素。
-
矩阵中列的个数是固定的。列可能是fixed、advice或者instance。Fixed列在电路中是固定的;advice列是论据信息;instance列通常用作公开输入(技术上讲, 它们可以是证明者和验证者之间共享的任何元素)。
-
一些列参与相等约束。
-
多项式阶的范围。
-
一系列多项式约束。这些多项式每一行在 上的取值为零。多项式约束中的变量可以是给定列当前行中的单元格,也可以是给定列中与这行相关的行(比如模)。每个多项式的最高阶由多项式阶的范围限定。
-
一系列的查找表论据,定义了查找表的输入和查找表相关的列。
PLONK化电路还定义:
-
矩阵的行数为 。 必须对应于的乘法子群的大小;通常是2的幂次。
-
一系列相等约束,指定两个给定单元格必须具有相等的值。
-
固定列中每行的固定值。
根据电路,我们可以生成电路证明和验证操作所需要的证明密钥 和验证密钥。
请注意,我们指定了列的顺序、多项式约束、查找表论据和相等约束,这些并不影响电路的含义。但这些使得证明和验证密钥的确定性的生成过程变得更加容易。
通常,配置将定义多项式约束,这些约束由定义在fixed列中的选择子关闭和开启。例如,一个约束 可以通过在第i行设置来关闭。在这种情况下,我们通常将多个选择子控制的一组约束,称一个门(gate)。通常标准门支持一些通用操作,比如域上的乘法和除法, 自定义门支持更专门的操作。
芯片
先前的章节介绍了一个低层的电路描述。在实现电路时, 我们通常会使用上层的API,这些API具有以可审核、高效、模块化和表达性强等特征。
在这些API中使用的一些术语和概念来源于集成电路的设计和布局。关于集成电路,通过组合特定功能的芯片更容易获得上述诸多特征。
举个例子, 我们可能有实现特定密码学原语的芯片,比如说哈希或者加密函数,或者像标量乘法或配对算法。
在UPA中,在实现了域上乘法和加法的标准门上可以构造任何电路逻辑。然而, 使用自定义门电路可以获得更高的效率。
采用我们的API, 我们可以设计使用自定义门的芯片。这些API是一个抽象层, 将上层的芯片设计和低层复杂的自定义门隔离开。
尽管有时我们需要 "身兼两职", 既要写上层的电路, 又要写上层电路所需要的芯片。这样做的目的是使代码更易于理解、审计和维护/重用。通过这种方法也排除了一些潜在的实现的错误。
UPA中的门通过相对引用 引用单元格,比如给定列中的某个单元格,或者某个选择子的相对偏移的单元格。当偏移非零时, 我们称之为 偏移引用 (也就是说, 偏移引用是相对引用的子集)。
和绝对引用 相反, 相对引用在相等约束中使用, 能指向任意单元格。
偏移引用的原因是减少配置中列的数量,从而减少证明的大小。如果没有偏移引用,则需要单独列来保存自定义门引用的每个值, 并我们需要使用相等约束,约束电路的其他单元格和该列中的单元格。使用偏移引用, 我们不仅需要更少的列, 我们也不需要为所有这些列增加约束,从而提高电路效率。
R1CS(对于一些读者来说,可能这个算术化更熟悉, 如果不是,也不要担心)电路包含了“海量的门”,这些门并没有语义上的顺序。 另一方面, UPA电路中的采用偏移引用, 行顺序非常重要。我们做一些简单的假定和定义一些抽象概念来控制电路结构复杂性: 小工具,内部实现电路构造,在小工具之间我们不采用相对引用或者特殊的门布局。
我们把一个电路分到多个区域 , 每一个区域都包含着一个不相交的单元格子集, 相对引用只在区域内使用。 芯片实现的部分职责是确保进行偏移引用的门被放置在区域的正确位置。
给定一些区域和他们的形状, 我们将使用一个单独的布局器 来决定每个区域放置在哪里(即起始行在哪里)。 目前实现了一个通用的布局器,如果有需要,你可以实现你自己的布局器。
布局器一般会在矩阵中留空一些区域, 因为在给定的行中,电路没有使用所有可用的列。 它们尽最大可能由不需要偏移引用的门填充。这些门可以被放置在一行中的任何位置。
芯片也定义了查找表。 如果同一个查找表论据中定义了多个表, 可以使用标记列指明每行使用了哪一个表。也可以把多个表组合成一张表(受多项式阶范围限制)进行查找。
芯片组合
为了将几个芯片的功能结合起来,我们将它们组合成树状。 最高层次的芯片定义fixed列、advice列和instance列,然后指定它们在较低层次芯片上的分布。
在最简单的情况下,每个底层芯片将使用与其他芯片不相同的列。然而,在芯片之间共享列也是允许的。优化advice列的数量尤其重要,因为这会影响证明大小。
芯片组合的结果(可能在优化之后)是一个UPA配置。电路实现将在芯片上参数化,并且可以通过上层芯片使用支持的底层芯片的功能。
我们希望不那么专业的用户通常能够找到支持他们需要的操作的现有芯片,或者只需要对现有芯片做微小修改。专家级用户可以自己实现电路优化。 ECC 以善于优化电路而闻名 🙂。
小工具
当实现一个电路时,我们可以直接使用我们选择的芯片的功能。 但通常,我们会通过小工具 使用他们。 这种间接方式是很有用的,因为由于效率和UPA的限制,芯片接口通常依赖于底层的实现细节。小工具接口可以提供更加方便和稳定的API,这些API可以从繁琐的细节中抽象出来。
举个例子,比如哈希函数SHA-256。 支持SHA-256的芯片接口可能是依赖于哈希函数的内部设计,例如message schedule和压缩函数的隔离。 相应的小工具接口可以提供更加方便和熟悉的 update/finalize API,也能够在不需要芯片支持的情况下支持hash函数的部分功能,比如说 补齐功能。这有点像CPU上的加速指令并不是直接访问,而是通过软件库调用。
小工具同时能为上层电路提供一个模块化,可重用的抽象,类似于在像 libsnark,bellman这样的库中的使用。 不光函数进行抽象,类型也进行抽象,例如特定大小的椭圆曲线上的点或整数。
用户手册
你来这里可能是因为你想写电路?太好了!
本节将指导你通过halo2创建电路的过程。
开发者工具
Rust库 halo2 中包含了数个工具,为你设计并开发自己的电路提供帮助。
Mock prover
halo2::dev::MockProver 是一个用来调试电路用的工具。除此之外,它还可以用来在单元测试中快速检验电路正确性。
隐私输入和公开输入的计算过程,是和生成一个真正的证明一样。但是,MockProver::run 函数只会生成一个对象,它直接检验电路中每一条约束是否满足。如果电路中某个约束不满足,那这个对象就会返回关于该约束的一个细粒度的错误信息。
消耗估算器
程序 cost-model 可以根据电路设计所采用的不同参数,估算出,验证一个证明的时长,以及对应的证明大小。
用法: cargo run --example cost-model -- [OPTIONS] k
Positional arguments:
k 2^k 总行数的上界.
Optional arguments:
-h, --help 打印此用法信息.
-a, --advice R[,R..] An advice column with the given rotations. May be repeated.
-i, --instance R[,R..] An instance column with the given rotations. May be repeated.
-f, --fixed R[,R..] A fixed column with the given rotations. May be repeated.
-g, --gate-degree D Maximum degree of the custom gates.
-l, --lookup N,I,T A lookup over N columns with max input degree I and max table degree T. May be repeated.
-p, --permutation N A permutation over N columns. May be repeated.
比如,估算有三个 advice列,一个 fixed 列(有相对引用)和门的最高次数为4的电路:
cargo run --example cost-model -- -a 0,1 -a 0 -a 0,-1,1 -f 0 -g 4 11
Finished dev [unoptimized + debuginfo] target(s) in 0.03s
Running `target/debug/examples/cost-model -a 0,1 -a 0 -a 0,-1,1 -f 0 -g 4 11`
Circuit {
k: 11,
max_deg: 4,
advice_columns: 3,
lookups: 0,
permutations: [],
column_queries: 7,
point_sets: 3,
estimator: Estimator,
}
Proof size: 1440 bytes
Verification: at least 81.689ms
一个简单例子
我们以一个简单电路为例,给大家介绍 halo2 所提供的应用编程接口,以及如何使用它们。示例电路有一个公开输入, 可证明知道两个隐私输入和,使得下式成立。
定义指令
首先,我们需要定义我们的电路所依赖的指令,指令介于高层的工具(gadgets)和底层的电路操作之间。指令既可以细粒度也可以粗粒度,但在实践中,指令的功能应当足够小,这样可以重复使用;但又要足够大,这样可以优化它的实现。设计者应当在这两者之间取得平衡。
在我们的样例电路中,我们将使用如下三种指令:
- 加载一个隐私数到电路中;
- 计算两个数的乘积;
- 将一个数设置为电路的公开输入。
我们还需要一个类型来表示其值为数的变量。
#![allow(unused)] fn main() { trait NumericInstructions<F: FieldExt>: Chip<F> { /// 用于表示一个数的变量 type Num; /// 将一个数加载到电路中,用作隐私输入 fn load_private(&self, layouter: impl Layouter<F>, a: Option<F>) -> Result<Self::Num, Error>; /// 将一个数加载到电路中,用作固定常数 fn load_constant(&self, layouter: impl Layouter<F>, constant: F) -> Result<Self::Num, Error>; /// 返回 `c = a * b`. fn mul( &self, layouter: impl Layouter<F>, a: Self::Num, b: Self::Num, ) -> Result<Self::Num, Error>; /// 将一个数置为电路的公开输入 fn expose_public( &self, layouter: impl Layouter<F>, num: Self::Num, row: usize, ) -> Result<(), Error>; } }
定义芯片的实现
在示例电路中,我还将构造一个芯片,其功能包含上述的有限域上的数值指令。
#![allow(unused)] fn main() { /// 这块芯片将实现我们的指令集!芯片存储它们自己的配置, /// 必要情况下也要包含 type markers struct FieldChip<F: FieldExt> { config: FieldConfig, _marker: PhantomData<F>, } }
每一个"芯片"类型都要实现Chip接口。Chip接口定义了Layouter在做电路综合时可能需要的关于电路的某些属性,以及若将该芯片加载到电路所需要设置的任何初始状态。
#![allow(unused)] fn main() { impl<F: FieldExt> Chip<F> for FieldChip<F> { type Config = FieldConfig; type Loaded = (); fn config(&self) -> &Self::Config { &self.config } fn loaded(&self) -> &Self::Loaded { &() } } }
配置芯片
需要为芯片配置好实现我们想要的功能所需要的那些列、置换、门。
#![allow(unused)] fn main() { /// 芯片的状态被存储在一个 config 结构体中,它是在配置过程中由芯片生成, /// 并且存储在芯片内部。 #[derive(Clone, Debug)] struct FieldConfig { /// 对于这块芯片,我们将用到两个 advice 列来实现我们的指令集。 /// 它们也是我们与电路的其他部分通信所需要用到列。 advice: [Column<Advice>; 2], /// 这是公开输入(instance)列 instance: Column<Instance>, // 我们需要一个 selector 来激活乘法门,从而在用不到`NumericInstructions::mul`指令的 // cells 上不设置任何约束。这非常重要,尤其在构建更大型的电路的情况下,列会被多条指令集用到 s_mul: Selector, /// 用来加载常数的 fixed 列 constant: Column<Fixed>, } impl<F: FieldExt> FieldChip<F> { fn construct(config: <Self as Chip<F>>::Config) -> Self { Self { config, _marker: PhantomData, } } fn configure( meta: &mut ConstraintSystem<F>, advice: [Column<Advice>; 2], instance: Column<Instance>, constant: Column<Fixed>, ) -> <Self as Chip<F>>::Config { meta.enable_equality(instance.into()); meta.enable_constant(constant); for column in &advice { meta.enable_equality((*column).into()); } let s_mul = meta.selector(); // 定义我们的乘法门 meta.create_gate("mul", |meta| { // 我们需要3个 advice cells 和 1个 selector cell 来实现乘法 // 我们把他们按下表来排列: // // | a0 | a1 | s_mul | // |-----|-----|-------| // | lhs | rhs | s_mul | // | out | | | // // 门可以用任一相对偏移,但每一个不同的偏移都会对证明增加开销。 // 最常见的偏移值是 0 (当前行), 1(下一行), -1(上一行)。 // 针对这三种情况,有特定的构造函数来构造`Rotation` 结构。 let lhs = meta.query_advice(advice[0], Rotation::cur()); let rhs = meta.query_advice(advice[1], Rotation::cur()); let out = meta.query_advice(advice[0], Rotation::next()); let s_mul = meta.query_selector(s_mul); // 最终,我们将约束门的多项式表达式返回。 // 对于我们的乘法门,我们仅需要一个多项式约束。 // // `create_gate` 函数返回的多项式表达式,在证明系统中一定等于0。 // 我们的表达式有以下性质: // - 当 s_mul = 0 时,lhs, rhs, out 可以是任意值。 // - 当 s_mul != 0 时,lhs, rhs, out 将满足 lhs * rhs = out 这条约束。 vec![s_mul * (lhs * rhs - out)] }); FieldConfig { advice, instance, s_mul, constant, } } } }
实现芯片功能
#![allow(unused)] fn main() { /// 用于表示数的变量 #[derive(Clone)] struct Number<F: FieldExt> { cell: Cell, value: Option<F>, } impl<F: FieldExt> NumericInstructions<F> for FieldChip<F> { type Num = Number<F>; fn load_private( &self, mut layouter: impl Layouter<F>, value: Option<F>, ) -> Result<Self::Num, Error> { let config = self.config(); let mut num = None; layouter.assign_region( || "load private", |mut region| { let cell = region.assign_advice( || "private input", config.advice[0], 0, || value.ok_or(Error::SynthesisError), )?; num = Some(Number { cell, value }); Ok(()) }, )?; Ok(num.unwrap()) } fn load_constant( &self, mut layouter: impl Layouter<F>, constant: F, ) -> Result<Self::Num, Error> { let config = self.config(); let mut num = None; layouter.assign_region( || "load constant", |mut region| { let cell = region.assign_advice_from_constant( || "constant value", config.advice[0], 0, constant, )?; num = Some(Number { cell, value: Some(constant), }); Ok(()) }, )?; Ok(num.unwrap()) } fn mul( &self, mut layouter: impl Layouter<F>, a: Self::Num, b: Self::Num, ) -> Result<Self::Num, Error> { let config = self.config(); let mut out = None; layouter.assign_region( || "mul", |mut region: Region<'_, F>| { // 在这个 region 中,我们只想用一个乘法门,所以我们在 region 偏移 0 处, // 激活它;这意味着它将对 0偏移 和 1偏移处的两个 cells 进行约束。 config.s_mul.enable(&mut region, 0)?; // 给我们的输入有可能在电路的任一位置,但在当前 region 中,我们仅可以用 // 相对偏移。所以,我们在 region 内分配新的 cells 并限定他们的值与输入 cells 的值相等。 let lhs = region.assign_advice( || "lhs", config.advice[0], 0, || a.value.ok_or(Error::SynthesisError), )?; let rhs = region.assign_advice( || "rhs", config.advice[1], 0, || b.value.ok_or(Error::SynthesisError), )?; region.constrain_equal(a.cell, lhs)?; region.constrain_equal(b.cell, rhs)?; // 现在我们可以把乘积放到输出的位置了。 let value = a.value.and_then(|a| b.value.map(|b| a * b)); let cell = region.assign_advice( || "lhs * rhs", config.advice[0], 1, || value.ok_or(Error::SynthesisError), )?; // 最后,我们返回一个用来表示输出的变量,它会被用在电路的另一个部分。 out = Some(Number { cell, value }); Ok(()) }, )?; Ok(out.unwrap()) } fn expose_public( &self, mut layouter: impl Layouter<F>, num: Self::Num, row: usize, ) -> Result<(), Error> { let config = self.config(); layouter.constrain_instance(num.cell, config.instance, row) } } }
构造电路
既然我们已经有了所需要的指令,以及一块实现了这些指令的芯片,我们终于可以构造示例电路啦!
#![allow(unused)] fn main() { /// 完整的电路实现 /// /// 在这个结构体中,我们保存隐私输入变量。我们使用 `Option<F>` 类型是因为, /// 在生成密钥阶段,他们不需要有任何的值。在证明阶段中,如果它们任一为 `None` 的话, /// 我们将得到一个错误。 #[derive(Default)] struct MyCircuit<F: FieldExt> { constant: F, a: Option<F>, b: Option<F>, } impl<F: FieldExt> Circuit<F> for MyCircuit<F> { // 因为我们在任一地方值用了一个芯片,所以我们可以重用它的配置。 type Config = FieldConfig; type FloorPlanner = SimpleFloorPlanner; fn without_witnesses(&self) -> Self { Self::default() } fn configure(meta: &mut ConstraintSystem<F>) -> Self::Config { // 我们创建两个 advice 列,作为 FieldChip 的输入。 let advice = [meta.advice_column(), meta.advice_column()]; // 我们还需要一个 instance 列来存储公开输入。 let instance = meta.instance_column(); // 创建一个 fixed 列来加载常数 let constant = meta.fixed_column(); FieldChip::configure(meta, advice, instance, constant) } fn synthesize( &self, config: Self::Config, mut layouter: impl Layouter<F>, ) -> Result<(), Error> { let field_chip = FieldChip::<F>::construct(config); // 将我们的隐私值加载到电路中。 let a = field_chip.load_private(layouter.namespace(|| "load a"), self.a)?; let b = field_chip.load_private(layouter.namespace(|| "load b"), self.b)?; // 将常数因子加载到电路中 let constant = field_chip.load_constant(layouter.namespace(|| "load constant"), self.constant)?; // 我们仅有乘法可用,因此我们按以下方法实现电路: // asq = a*a // bsq = b*b // absq = asq*bsq // c = constant*asq*bsq // // 但是,按下面的方法实现,更加高效: // ab = a*b // absq = ab^2 // c = constant*absq let ab = field_chip.mul(layouter.namespace(|| "a * b"), a, b)?; let absq = field_chip.mul(layouter.namespace(|| "ab * ab"), ab.clone(), ab)?; let c = field_chip.mul(layouter.namespace(|| "constant * absq"), constant, absq)?; // 将结果作为电路的公开输入进行公开 field_chip.expose_public(layouter.namespace(|| "expose c"), c, 0) } } }
测试电路的功能
可以用 halo2::dev::MockProver 对象来测试一个电路是否正常工作。构造电路的一组隐私输入和公开输入,这组输入可直接用来计算合法证明,但我们把这组输入传入到MockProver::run函数中之后,就能得到一个可用于检验电路中每一条约束是否满足的对象。而且电路验证不过,这个对象还能输出那条不满足的约束。
#![allow(unused)] fn main() { // 我们电路的行数不能超过 2^k. 因为我们的示例电路很小,我们选择一个较小的值 let k = 4; // 准备好电路的隐私输入和公开输入 let constant = Fp::from(7); let a = Fp::from(2); let b = Fp::from(3); let c = constant * a.square() * b.square(); // 用隐私输入来实例化电路 let circuit = MyCircuit { constant, a: Some(a), b: Some(b), }; // 将公开输入进行排列。乘法的结果被我们放置在 instance 列的第0行, // 所以我们把它放在公开输入的对应位置。 let mut public_inputs = vec![c]; // 给定正确的公开输入,我们的电路能验证通过 let prover = MockProver::run(k, &circuit, vec![public_inputs.clone()]).unwrap(); assert_eq!(prover.verify(), Ok(())); // 如果我们尝试用其他的公开输入,证明将失败! public_inputs[0] += Fp::one(); let prover = MockProver::run(k, &circuit, vec![public_inputs]).unwrap(); assert!(prover.verify().is_err()); }
完整例子
这里 有示例的所有源代码。
查找表
在正常的程序中,你可以采用内存换CPU的方法来提高性能,即为计算的某一部分预计算出查找表,并存在内存中。我们也可以在 halo2 电路中实现类似的策略。
我们可以将一个查找表理解成变量之间存在一个关系,该关系可以表示成一个表。假设在我们的约束系统中仅有一个查找证明,那么查找表的总大小的上限为电路规模,即每一个表项占用一行,每一个表查找占用一行。
实用的小方法
本节包含几个写 halo2 电路时能用帮上忙的小策略。
小范围(or 区间?)约束
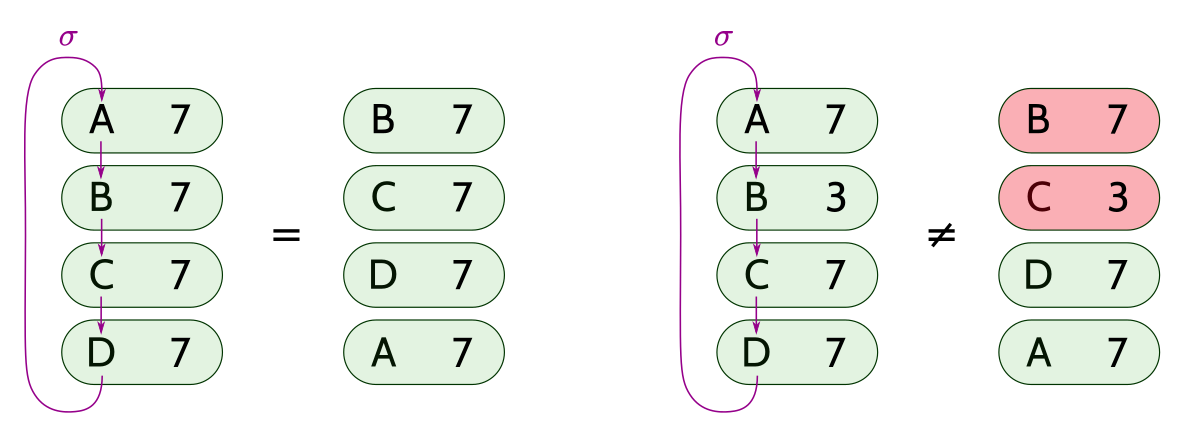
在 R1CS 电路中,经常用到的一种约束就是布尔约束: . 这种约束限定了 或者 .
类似地,在 halo2 电路中,你也可以限定一个 单元格 在一个小集合内取值。比如,若要限定 的值落在区间 ,你可以构建如下形式的门:
又比如,要限定 等于 7 或 13,你可以用如下的门:
基本原理就是,我们构建一个多项式约束,使得其根集合与我们想限定的取值集合相同。 R1CS 电路支持的多项式次数最大为2(因为所有的约束方程必须具有 的形式)。 而 halo2 电路支持任意次数的多项式,只不过更高次数会带来更大的代价。
需要注意,这些根不必是常量;比如,可以用 来限定 等于集合 中的任一元素。而且,
小集合插值
我们可以用 Lagrange 插值法构造一个多项式约束,证明 ,其中 。
例如,假设我们想把两个比特的值通过插零扩展为“Spread”4个比特值。我们首先预计算出每一个点上的取值:
然后,为每一个点计算出对应的 Lagrange 基多项式(basis polynomial),其中 是点的个数(在我们的例子中,):
回顾一下,Lagrange 基多项式 满足如下性质:若 , 则 ;否则,,一定有 。
回到我们刚才举的例子,我们就计算出了4个 Lagrange 基多项式:
那么,我们就得到了如下所示的多项式约束:
设计
语言方面的注解
我们用和其他语言稍微不同的语言描述PLONK的相关概念。总体上:
- 我们把PLONK相关的证明看成表,每一列对应一根“线”。表中元素我们称为“单元格”。
- 我们喜欢说“选择子多项式”和“固定列”。当一个在固定列的单元格用来控制一个行中的约束是否开启的时候,我们称“选择子约束“。
- 其他多项式,我们称为”advice列“。这些列由证明者提供。
- 我们用”规则“字眼表述一个”门“,比如
- TODO: Check how consistent we are with this, and update the code and docs to match.
证明系统
Halo2的证明系统可以分解成五个部分:
- 对电路中的主要模块多项式承诺:
- 单元格的赋值
- 查找表证明中的置换和乘积
- 相等约束的置换
- 电路中和零相关的部分,构造消退证明:
- 标准的和自定义门
- 查找表规则
- 相等约束规则
- 在所有需要的点上,获取上述多项式的取值:
- 所有自定义门上的偏移信息
- 消退证明的各个部分
- 构建多点打开证明,检查所有的多项式取值和相应的承诺是否一致
- 采用内积证明为多点打开证明生成证明
这些部分依次在本章节讲解。
举个例子
为了辅助我们的解释,我们时不时地用如下的约束系统:
- 四个advice列
- 一个fixed列
- 三个自定义门:
太长不读
Halo2协议的简洁描述整理在如下的表格中。这部分会被Halo2的论文和安全性证明替代,目前作为后面子章节的总结:
| 证明者 | 验证者 | |
|---|---|---|
| 检查 | ||
| 构造 多点打开多项式 | ||
Then the prover and verifier:
- Construct as a linear combination of and using powers of ;
- Construct as the equivalent linear combination of and ; and
- Perform
TODO: Write up protocol components that provide zero-knowledge.
查找表(Lookup)论据
halo2实现任意集合的数据查找,相比Plookup简单。
语言(Language)说明
除了 语言的一般说明:
- 多项式(针对置换论据的大乘积论据多项式)称为“置换乘积”列。
技术描述
为了解释简单,我们先描述一个忽略零知识证明的论据描述的简单版本。
查找可以表示成 行表(编号从0开始)的“子集”。和列分别是“子集”和“全集”。
“子集”论据保证列中的元素都在 列中。这意味着,列中多个位置的元素对应着列中同一位置的元素,并且列中的某些元素可以不出现在列的任何位置上。
- 列并不一定是固定的。也就是说,我们可以支持固定元素的查找或者动态查找(后者采用advice列)。
- 和列中的元素可以重复。如果 和列中的元素个数不正好是的话,可以用 和列中任意元素进行扩展。
- 或者我们可以增加一个“查找选择子”,控制在列中的哪些元素参与查找。采用这种方法可以替换下述公式中的 。如果一个元素不需要查找,用替换。
假设 是拉格朗日基多项式,在行多项式为1,其他行为0。
从 和列的置换开始。假设它们的置换分别为 和 列。我们可以通过置换论据约束它们之间的置换关系:
也就是说,在除以0不发生的情况下,对所有的满足:
这个版本的论据证明 和 列是 和列的置换,但是并没有指明具体的置换关系。 和 是独立因子。采用这两个因子,可以将两个置换论据组合在一起,不需要担心相互干扰。
这些置换的目的是让证明者提供的 和 列满足一定的条件:
- 列中相同的元素位置靠在一起。这可以通过某种排序算法实现。重要的是,相同的元素在列中挨在一起,并且列是列的置换。
- 列中挨在一起的相同元素的第一个元素存在于列中。除去这个限制外,列是列的一个任意置换。
现在我们通过如下的规则限制 或者 :
除此之外,我们通过如下的规则限制:
由于第二个规则,第一个规则中的( 这一项在行没有效果,尽管 “能反转”。
这些约束规则一起有效的限制了列(也就是列)中的每个元素都存在于 列中(也就是列)。
加入零知识
为了在PLONK算法为基础的证明系统中加入零知识,我们需要在每列的最后加入个随机元素。这些需要对查找论据进行调整,因为这些随机的元素并不满足之前的约束。
我们限制有效的行数为。我们增加两个选择子:
- 在最后 行设置为1,其他行设置为0;
- 只在行设置为1,其他行设置为0 (也就是说,它设置在有效行和盲化行的交界处)。
我们将之前的规则限制在有效行上:
在行的限制规则保持不变:
因为我们不能再依赖在 点的环绕保证为1,相反我们要约束 为1。这里有个难点:如果在任意, 或者 为0的话,置换论据可能不成立。虽然这种情况在 和的取值下概率可以忽略,但是,对于完美零知识和完备性来说是个障碍(攻击者可以构造这样的情况)。
确保完美的完备性和零知识,我们允许为0或者1:
如果 和 在某些 上为0,我们可以在范围设置,满足上述的约束。
注意的是,挑战因子 和 是在 和列(以及 和 列)承诺后生成的,证明者无法伪造 和 为0的情况。因为这种情况的概率可以忽略,可行性不受影响。
开销
- 原始列和固定列。
- 置换函数 。
- 两个置换 和 列。
- 约束方程(门)的阶都不高。
泛化
halo2的查找论据实现实现了上述技术的泛化:
- 和列扩展为多列,这些列之间通过随机挑战因子进行组合。 和 列还是单列。
- 列的各列承诺可以提前计算。这样在挑战因子确定后,利用Pedersen承诺的同态性质,可以很简便的组合成列的承诺。
- 列可以是采用相对引用的任意多项式表达式。这些可以替换到约束规则中去,受制于最大的阶。这样可能可以省去一个或者多个advice列。
- 这样的话,查找论据可以通过子集论据实现任意长度的关系。也就是说,为了约束,将看成是(通过前面的方法),并且检查关系成立 。
- 如果代表一个函数,同样需要检查输入是否在域中。这是我们想要的,经常会省去额外的范围检查。
- 我们可以在同一个电路中支持多表。利用标示列将多个表组合成一张表。
- 标示列可以和之前提到的“查找选择子”合并。
这些泛化和Plookup论文的第4和第5节中的技术类似。和Plookup的区别是子集论据。相关技术,子集论据也适用;举个例子,Plookup论文的第5节中的优化范围检查技术同样可以用在子集论据中。
置换证明
假设halo2电路中的门要“本地”操作(就是在当前行或者事先定义好的相关行进行操作) 这通常需要将某个任意单元格的值拷贝到当前行,以便在门中使用。该工作就由一条相等约束来描述, 该约束就强制要求源和目的单元格中包含相同的值。
我们通过构造一个代表这些约束的置换来实现这些相等约束,进而在最终的证明中包含一个置换证明来确保约束成立。
相关记号
置换就是一个集合以一对一的方式自己到自己的一个映射。一个置换可以唯一分解成多个轮换的组合(每个轮换都是首尾相接的,轮换和轮换之间排序)。
通常,我们使用 轮换记号 来表示置换。令 代表如下轮换: 映射到 , 映射到 , 映射到 (显然,该法则可以推广到任意大小的轮换)。把两个或更多的轮换一个接一个的写在一起就代表了一个相关置换的组合。 比如, 就代表了 映射到 , 映射到 , 映射到 , 映射到 的置换。
构造置换
目标
我们希望构造这样一个置换,在同一个相等约束下的这些变量自己形成一个轮换。举例来说,假设我们有一个定义了如下相等约束的电路:
由上可得相等约束集合 和 。于是我们构造了如下的置换:
该置换就定义了一个由 到 的一个映射。
算法
我们需要持续记录这些轮换的集合,实际上也就是 一些不相交集合的集合. 我们已经知道针对该问题的一种高效的数据结构;为了简单起见,我们选择了一个虽然不是渐进最优,但是确是很容易实现的方法。
我们采取如下方法来表示当前的状态:
-
数组 来表示置换本身;
-
一个辅助的数组 用来记录每个轮换中代表元素;
-
还有一个数组 用来记录每个轮换的元素个数。
我们在一个给定的轮换 中选取一个不变的值 ,对每一个 中的元素 , 都得到相同的值,即 。有了这个值,对于给定的两个给定的元素 和 ,我们可以通过检查 是否成立,来快速判断它们是否在同一个轮换中。 也代表了包含 的轮换的大小。(只有 是有保证的,而不是 。)
本算法是以表示一个单位置换开始: 对所有 ,我们令 ,,和 。
按如下步骤增加一条相等约束 :
-
检查 和 是否已经在同一个轮换中了,也就是检查 是否成立。如果是此种情况,那么不许做任何事情。
-
否则, 和 就一定分属不同的轮换。令 是相对大的轮换,而 则为相对小的那个, 如果 ,那我们就交换一下使其满足需求。
-
令 。
-
下一步对right(较小的)轮换中每一个元素 令 。
-
通过交换 和 中的元素(的轮换),将较小的轮换接入到较大的轮换中去。
举个例子,假设两个不相交的轮换 和 :
A +---> B
^ +
| |
+ v
D <---+ C E +---> F
^ +
| |
+ v
H <---+ G
在增加约束 后,上文算法将得出如下的轮换:
A +---> B +-------------+
^ |
| |
+ v
D <---+ C <---+ E F
^ +
| |
+ v
H <---+ G
Broken alternatives
如果不检查 和 是否在同一个轮换中,那么我们可能就会丢掉某些相等约束。 举个例子,如果我们有如下的约束:
如果在处理一条新的相等约束时仅仅只执行上述算法中的第五步,那么我们得到的最终结果将是 ,而不是正确的结果 。
证明说明
我们需要检查 列中所有单元格的置换,该 列分别由其拉格朗日基的多项式 来表示。
我们用 中不同的元素来标记 列中 每个单元格。
假设我们有基于这些标记的一个置换: 其中这些轮换就对应了相等约束。
我们考虑对 的集合,当且仅当对每对的label都按照 进行置换后,得到了与原集合相同的集合, 才能证明集合中的每个对是相等的。
因为所有的标记都是不同的,最终就可以用一个代表相等约束的集合来代替多个代表相等关系的集合,而这进一步使我们可以用乘积证明来检查置换的正确性。
令 是 次单位根, 是 次单位根,满足 ,其中 是奇数并且 。 在置换证明中,我们用 作为第 行、第 列的单元格的标记。
由 个多项式组成的一个向量,其中对每一项 满足 。
注意,可以用一个包含 个多项式的向量来标识一个置换,其中每一项 都满足 。
我们用一个挑战 将每一个 对压缩成 。与在 查找表 的积证明中所做的一样,我们也使用一个挑战 来盲化我们每一个积项。
假定有一个在 列,即: 上的一个置换,表示为 ,我们想要确保如下等式成立:
上式中 代表置换前的对 , 则代表其置换的对 。
令多项式 满足 并且对 :
接下来只需要强制满足如下的规则对证明来说就足够了:
注意,上述第一条规则对其处理的多项式的假设是,其约束的列数 要符合PLONK设置的次数界限。接下来,将在下文阐述如何处理列数超出边界的情况。
用于表示一个置换的经过优化的简单方法是由Vitalik Buterin为 PLONK 提出的,并且在 PLONK 论文的第8节有阐述 注意在实践中,对 Halo 2 所用的曲线来说,其有相等约束的列数通常不会超过其边界 , 在此条件下,所有的 就都是不同二次平方非剩余。
零知识调整
与查找表证明类似,我们也需要调整上述的证明来处理每列的最后 行,因为它们被填入了随机值(也就是这些行不满足上面的积证明)。
我们限定有用的行数是 ,同时我们增加两个选择子,这两个选择子与查找表证明中定义的是一样的:
- 只在最后 行设为 ,而在其他地方则为 。
- 则旨在 行设为 ,其他行则为 (这就是说,它只在有用行和盲化行之间的那一行起作用)。
我们将在那些有用的行真正应用上文的积规则:
在 行的的规则仍然是相同的,即:
由于我们再也不能依赖全景来确保每一个积证明 都在 等于 ,那么我们实际上应该约束 。这也就带来了在查找证明中同样的问题。于是,我们也就需要允许 等于 或者 :
通过这种方式,我们就获得了良好的完备性和零知识性。
支持大列
在halo2的实现中,实际上并不限制相等约束可以占用的行数。因此,就必须解决上述方法中可能导致的积规则中的多项式可能超出PLONK设置的次数边界的问题。一个简单办法是直接升高次数边界,但是在没有其他规则需要用到如此大的次数的情况下,这一办法是低效的。
另一种方法,我们把积证明分割成 个,每个都是其中 列的证明,即:同时增加一条规则,就是每个积(证明)最终的积被设置成下一个积(证明)的起始值。
这就是说,对于 我们有:
简单起见,上述规则假设总列数是 的整数倍; 如果不是,那么我们就让最后一个列集合少于 个项。
对第一个列集合,我们有
而对于剩余的每一个列集合 ,我们将使用如下规则将 拷贝到下一个列集合的最开始,:
与起始算法相同,对最后一个列集合,我们约束 为 或者 。
与上文的证明相同,这也提供了同样的完备性和零知识性。
电路承诺
对电路赋值进行承诺
在生成证明之前,证明者已经有了一张能够满足约束条件的单元格赋值表。赋值表有 行;其列被划分为三类: advice, instance, fixed 。我们定义 表示第 行的第 个fixed列,不失一般性,定义 为第 行的第 个advice或instance列。
我们区分开fixed 列的原因是它们是由验证者提供的,而advice 列和instance 列是由证明者提供的。实际上,证明者和验证者都需要计算instance 列和fixed 列的承诺,只有对advice 列的承诺在证明中。
为对表中的各个赋值进行承诺,我们为每列构造一个次数为 的拉格朗日多项式,其取值域大小为 (令 为其 次单位根)。
- 令 ,通过插值得到 多项式
- 令 ,通过插值得到 多项式
然后对每列的多项式创建一个盲化承诺(blinding commitment) :
其中 在生成密钥的时候被创建,使用 作为盲因子。 由证明者计算并发送给验证者 。
对查找表置换进行承诺
验证者随机选择一个 ,用于确保同一个查找表内不同的列线性无关。接着证明者对每个查找表的置换进行承诺
-
给定一个查找表,其输入列多项式为 ,其真值表列的多项式为 , 证明者构造两个压缩后的多项式
-
之后证明者对 和 依照 查找表证明 的规则进行排列,得到 和 .
证明者为所有的查找表创建盲化承诺:
并发送给验证者 。
当验证者接收到 , ,和 后,随机采样 和 作为挑战,用于后续的置换和查找表证明验证。(随机采样是可以重复利用的,因为证明是相互独立的)。
对相等约束置换进行承诺
令 为 相等约束所涉及的列数。
令 为能容纳的 最大列数 , 不能超过 PLONK 配置中多项式的次数上限。
令 为 置换证明 章节中定义的可以“使用”的行数。
令
证明者构造一个长度为 的向量 ,对于每个列集合,有, ,对于每一行有
证明者计算 的”滚动乘积“, 从 开始,并且多项式向量 每个都有拉格朗日基表示,基于滚动乘积的长度为 的切片,如 置换证明 章节中所描述的。
最后 证明者为每个 多项式创建盲化承诺:
并发送给 验证者 。
对查找表置换进行承诺
除了需要对单独的相等约束进行承诺外,对每一个查找表, 证明者也需要对置换进行承诺。
- 证明者构造一个向量 :
- 证明者构造多项式 ,其拉格朗日基表示为 多项式的“滚动乘积”,从 开始。
和 用于在组合 和 的同时保持这两者无关。 和 是验证者在证明者创建多项式 , ,和 之后采样的(因此承诺了在 查找表列中用到的单元格的值,以及每个 查找表的 和 )。
如之前一样, 证明者对每个 多项式都创建一个盲化承诺并发送给 验证者 :
消退证明
在电路的所有赋值都已经承诺之后,证明者现在需要证明各种各样的电路关系都是满足的:
- 自定义门,用多项式 表示。
- 查找证明的约束
- 相等约束置换的约束
从电路的列的角度看,每个关系都由一个 次多项式表示(在所有关系中最大的的次数。假设对应一列的赋值多项式的次数是 ,那么从 的角度看,关系多项式的次数就是
在我们的例子中,门多项式的次数是 。
如果描述关系的多项式为 ,我们就说关系是满足的。一种表示这种此种约束的方法,就是将每个多项式关系都除以消除多项式 ,消除多项式是以 作为根的最低次数的单项式。如果关系多项式能被 整除,那么在域上这个关系多项式就等于 。
这种朴素的构造方式的弊端在于,其需要对每个关系都需要有一个多项式承诺。相反,我们可以对电路中所有关系同时进行承诺:验证者取一个 ,然后证明者构造一个商多项式,
其中分子是电路关系的随机的线性组合(证明者需要在验证者给出 之前先承诺单元格赋值)。
- 如果分子多项式(以 为自变量)能够被 整除,那么所有的关系都满足的概率就是非常高的
- 相反地,哪怕只有一个关系是不满足的,那么在点 处, 与分子多项式在该处的值就几乎不可能相等。也就是说,在此种情况下,分子多项式不能整除 。
承诺
的次数是 (因为分母 的次数是 )。但是我们在 Halo 2 中的多项式承诺机制仅仅支持次数 次的多项式的承诺(这是因为除了关系多项式的承诺,协议其他部分所需承诺的多项式的最大次数就是 )。为了不给多项式承诺机制增加额外的成本,验证者就需要把 分割成多个,每个只有 次的多项式的和,
并对每一部分产生一个具有隐藏承诺。
多项式求值
到这一步,电路所有的特点都已经被承诺了。现在,验证者想要验证一下证明者提供的承诺是不是正确的 。于是,验证者选取一个 ,证明者需要提供其所声称的所有多项式在 处的值,包括电路中使用的所有相对偏移和 的值。
在我们的例子中,这就是:
- ,
- ,
- , ...,
验证者现在要验证这些值是不是满足 的形式:
如果这些值确实满足的门约束,那么验证者接下来就需要验证这些值本身与最初的电路承诺以及承诺 是否一致。为了高效实现此一目的,我们使用了多点打开证明。
多点打开证明
假设 分别是多项式 的多项式承诺值。比如说,我们要打开多项式 在点的取值,与此同时,打开 在两个点 的取值。(此处的 是乘法子群的本原单位根)。
比较容易想到的方法是,为每一个点构造一个多项式(每一个打开点就会对应电路中的一个相对转动(rotation))。但这不是一个有效的方法;比如, 会出现在多个多项式中。
相反地,我们按打开点的集合,将多项式承诺值组织在一起:
对于每一个组,我们将这些多项式合并成一个多项式集合,然后构造一个多项式, 并在该点打开所有相对偏移。
优化步骤
多点打开的优化算法的输入为:
- 验证者采样出一个随机点,我们将计算多项式在该点的值;
- 证明者计算出那些我们想要的多项式点值:。
这些数据是 vanishing证明 的输出。
多点打开优化算法的步骤如下:
-
采样一个随机点,用来让 线性无关;
-
对于每一个点集,将对应的多项式集合聚合成一个多项式,得到新的多项式集合
q_polys。同理对于每一个点集,也计算出新的多项式点值集合
q_eval_sets。
[
[a(x) + x_1 b(x)],
[
c(x) + x_1 d(x),
c(\omega x) + x_1 d(\omega x)
]
]
-
根据
q_eval_sets,构造插值多项式集合r_polys: -
构造
f_polys来检查q_polys的正确性:如果 ,则 应当是一个多项式; 如果 并且 ,则 应当是一个多项式。
-
采样一个随机数 ,用来让
f_polys线性无关。 -
构造 。
-
采样一个随机数,并计算在该点的取值:
-
采样一个随机数,用来让 和
q_polys线性无关。 -
构造
final_poly多项式 \textrm{final_poly}(X) = f(X) + x_4 q_1(X) +x_4^2 q_2(X)final_poly多项式就是传入内积证明的多项式。
内积证明
Halo2 使用的多项式承诺算法,其多项式承诺打开证明是基于内积证明的。
待办事项:解释 Halo2 所使用的IPA变体。
与其他工作的比较
BCMS20 附录 A.2
BCMS20 附录 A.2 提出了一种与 BGH19 中类似的多项式承诺机制(BCMS20 是对原始的 Halo 论文的推广)。 Halo 2 这些工作的基础上,因此其自身也就使用了一种与 BCMS20 中很类似的多项式承诺机制。
下表提供了一个BCMS20和Halo 2中具有相同含义的变量的对照表(Halo 2的术语是建立在Halo论文基础上的):
| BCMS20 | Halo 2 |
|---|---|
msm or | |
challenge_i | |
s_poly | |
s_poly_blind | |
s_poly_commitment | |
blind / | |
Halo 2的多项式承诺机制与BCMS20附录A.2的机制有两点不同:
-
算法的第8步将在内积证明之前计算一个“非隐藏”的承诺 。 该承诺与 拥有相同的打开之,只不过它是仅是一个对一个随便写的多项式的承诺。 协议的剩余部分则是没有盲化的。与之相比,Halo 2中我们会盲化我们产生的所有的承诺(即便对于instance和fixed多项式也是如此, 尽管对fixed多项式的盲化因子是1),这使得协议更容易推理(???)。该方法的结果是,验证者在协议的最后要去 处理累计的盲化因子,所以在协议一开始就推导一个(与第一种方法)等价的 就没有必要了。
- is also an input to the random oracle for ; in Halo 2 we utilize a transcript that has already committed to the equivalent components of prior to sampling .(???)
-
The subroutine (Figure 2 of BCMS20) computes the initial group element by adding , which requires two scalar multiplications. Instead, we subtract from the original commitment , so that we're effectively opening the polynomial at the point to the value zero. The computation is more efficient in the context of recursion because is a fixed base (so we can use lookup tables).
-
子程序 (BCMS20的图2所示) 会通过增加 来产生最开始的群元素 ,而这需要两次scalar乘。与之不同,我们的方法是用最初的承诺 减去 ,如此 我们就可以在0处很高效地打开多项式。而的计算在递归证明的情况下具有更高效率,这是因为 是一个固定的基 (所以我们可以用查表(lookup tables)方法)。
Halo2 协议
预备工作
我们定义 作为一个安全参数,且除明确标注外,文档中所有的算法和敌手(adversaries)都是在该安全参数下运行时间为多项式的概率型图灵机。我们使用 表示一个在 下可忽略的函数。
密码学群
我们令 表示一个阶为素数 的循环群,群的单位元记作 。将 中元素的标量表示为阶为 的标量域 中的元素。群元素用大写字母表示,标量则用小写字母或希腊字母表示。群元素或标量所组成的向量用粗体字表示,例如 以及 。群上的运算记作加法,群元素 和标量 的乘法记作 。
我们会经常使用 表示长度相等的, 上 两个向量的内积。同样地也用这种表示法描述群元素的一个线性组合 ,其中 ,该内积的计算是通过群中的标量乘法和加法实现的。
我们使用 描述域 中长度为 的,只包含零元的向量。
离散对数关系问题 攻击者优势(advantage)的度量(metric)为: 其定义为赢得以下游戏的概率。 即:如果攻击者能够给出一个 使得 ,则它赢得这次游戏
给定一个长度为 的向量 , 离散对数关系问题 指寻找一个 使得 且 (我们称为 非平凡 离散对数关系)。该问题的难度和群中的离散对数问题紧密相连([JT20] 引理3)。我们使用上面定义的游戏 描述该问题。
交互式证明
交互式证明是一个算法三元组 。 算法用于生成某些被 引用的 公开参数 。证明者 和验证者 是能够访问 的交互式机器,我们用 表示在 和 之间执行的两方协议,其输入为 和 。协议的输出是一个 transcript ,包含了所有 和 之间交互的消息。在协议的最后,验证者输出一个决策位,表示它是否接受证明者的证明。
关于知识的零知识证明
知识证明是一种交互式证明,指证明者试图向验证者证明它知道一个 witness 使得 ,其中 为一个 statement , 为多项式时间内可决定的 relation。我们假设证明者的计算能力是有限的,在这个假设下研究知识证明。
我们将从四个角度分析知识证明的安全程度:
- 完备性: 如果证明者有一个有效的 witness ,它是否 总是 能够向验证者证明这一点?完备性做出了一些假设,理解完备性将有助于理解其他的安全性
- 可靠性: 一个试图作弊的证明者能否向验证者成功证明一个错误的 statement ? 我们将发生这种情况的可能性称为 可靠性错误 。
- 知识可靠性: 当验证者确信 statement 是正确的时候,证明者是否实际拥有(“知道”)一个有效的 witness ?我们将验证者确信,但证明者并不拥有有效 witness 的可能性称为 知识错误 。
- 零知识性: 除了 statement 的正确性和证明者实际拥有该有效 witness 之外,验证者是否还获得了额外的知识?
首先,我们考察完备性的一个简单定义:
完美完备性: 一个交互式证明 是 完美完备的 当对于所有的多项式时间内可决定的关系 和所有非均匀的多项式时间攻击者 都有
可靠性
我们分析过程的复杂性在于:我们的协议被描述为交互式证明,但实际上通过 Fiat-Shamir 变换,它被实现为 非交互式 的。
Public coin: 我们将那种验证者发送的每个消息都来自新的随机性采样的交互式证明称为 public coin 式。
Fiat-Shamir 变换: 将验证者发送的消息替换为密码学上健壮的哈希函数以产生足够的随机性,即可将交互的 public coin 式证明在 随机预言机模型 中转换为 非交互式 的。
这种形式变换意味着在实际的协议中,一个试图作弊的证明者可以通过对 transcript 进行分叉,修改某个时刻自己应该发送给验证者的消息,从而轻易的达成状态“回卷”。因此,研究我们的协议在 Fiat-Shamir 变换之后的安全性是非常重要的。幸运的是我们可以依照 Ghoshal 和 Tessaro 提出的框架 ([GT20]) 来进行分析。
我们通过 状态恢复可靠性 的概念分析我们的协议。在该模型中,(作弊的)证明者可以“回卷”验证者至之前任意的状态。如果证明者能通过这种方式使验证者接受证明,则是对我们协议一次成功的攻击。
状态恢复可靠性: 令 是一个交互式的 argument ,包含有 个验证者挑战。令第 th 个挑战是从 中采样获得,则一个具备状态恢复能力的证明者 的优势度量(advantage metric)为 通过以下攻防游戏定义:
如 [GT20] (定理1)所示,状态恢复可靠性和 Fiat-Shamir 变换后的可靠性紧密相关。
知识可靠性
我们将会展示我们的协议满足一种强知识可靠性,即 witness extended emulation 。这意味着,对于任意成功证明的证明者算法,都存在一个高效的仿真器,通过状态“回卷”和提供新的随机数,仿真器可以从算法中提取出 witness 。
但我们必须调整一下我们对于 witness extended emulation 的定义,以描述一个事实,即我们协议中的证明者都是有状态恢复能力的证明者,能够“回卷”验证者。另外,为避免在提取 witness 时回卷证明者,我们在 代数群模型 中研究我们的协议。
代数群模型(Algebraic Group Model, AGM) 若攻击者 在每次输出群元素 的时候同时也输出 在 中的一个 表示 ,使得 , 是 到目前为止所知的群元素的向量,则我们说 是 代数的 。
我们用 描述一个以代数方法表示的群元素 ,定义 为 用 表示的系数,即
代数群模型允许我们对某些协议进行所谓的“在线”提取:提取者可以从某个被接受的 transcript 的表示方式中提取出 witness 。
状态恢复的 witness extended emulation 令 是一个关系 的交互式证明,包含 个挑战。我们对所有非均匀的代数证明者 ,提取者 ,以及拥有无限计算能力的辨别者 ,其优势度量 定义为赢得如下游戏的概率:
零知识性
若验证者在协议的交互中除了知道存在一个有效的 之外没有获得任何其他额外的知识,则我们说该关于知识的证明是 零知识性 的。
完美特殊诚实验证者零知识性 一个交互式的 public coin 证明 拥有 完美特殊诚实验证者零知识性 (PSHVZK) 仅当对于所有多项式时间可决定的关系 和所有 及所有非均匀多项式时间的攻击者 , ,存在一个概率性的多项式时间模拟器 ,使得 表示 verifier 内在的随机性。
在这个零知识性的定义下,验证者预期将会“诚实地”进行交互,并发送只与它的内在随机性相关的挑战。它们不能根据证明者发送的消息改变自己的挑战。我们使用该定义的一种增强形式,要求模拟器输出包含和验证者所发送的相同挑战的 transcript 。
协议
令 是 的单位根,组成一个 domain , 为该 domain 上的消退多项式。令 为正整数。对于关系
我们提出一种交互式证明 ,其中 是关于 的阶为 的(多变量)多项式, 是关于 的阶为 的多项式。
返回 .
对于所有的 :
- 令 为整数 (模 )的完备集,使得 为 中的成员。
- 令 为一组包含 的不相交的整数集合, .
- 令 ,若 .
令 表示集合 的大小,不失一般性地,令 表示每个 集合的大小。
在下述的协议中,我们默认每个 多项式为 个盲因子均为验证者新采样的,且以 domain 上各点值的形式表示。
- 和 进行 轮交互,在第 轮中(轮次从0开始)
- 设置
- 发送一个隐藏用的承诺 , 其中 为单变量多项式 的系数, 为某个随机且独立采样的盲因子。
- 回应 一个挑战 .
- 和 设置 .
- 发送一个承诺 ,其中 为随机采样的单变量多项式 的系数,其度数为 。
- 计算单变量多项式 ,其度数为 .
- 计算度数至多为 的多项式 ,使得 .
- 将所有的承诺 发送给 ,其中 为多项式系数组成的向量。
- 回应一个挑战 并计算 .
- 设置 .
- 发送 并且对所有的 ,发送 ,使得对所有的 ,都有 。
- 对所有的 , 和 设置 为度数最低的单变量多项式,使得对所有的 , 。
- 发送两个挑战 以回应,并初始化 .
- 从 到 , 设置 .
- 最后 设置 .
- 初始化 .
- 从 开始到 , 设置 .
- 最后 设置 .
- 和 初始化 .
- 从 开始到 , 和 设置 .
- 最后 和 设置 , 使用由 提供的 和 计算
- 发送 ,其中 为下列多项式的系数:
- 回以挑战 .
- 发送 使得 for all .
- 回以挑战 .
- 和 设置 ,
- 设置 .
- 采样一个随机的度数为 的多项式 (其中一个根为 ) ,并发送其承诺 , 为 多项式的系数。
- 回以挑战 .
- 和 设置 .
- 设置 .
- 初始化 作为多项式 的系数,令 , . 和 将以如下方式交互 轮, 的取值范围从 到 :
- 发送 and .
- 回以挑战 .
- 和 设置 且 .
- 设置 .
- 发送 以及盲因子 .
- 若 ,则 接受证明。
Implementation
Halo2 证明
透明字节流形式的证明
在 bellman 这样的证明系统实现中,存在一个 Proof 结构体,用以封装证明数据,由 prover 返回且可以被传递给 verifier 。
但是 halo2 的实现中不存在类似的数据结构,理由如下:
Proof结构体需要包含椭圆曲线点和各标量的向量(以及向量的向量)。这会使证明的序列化/反序列化变得复杂,因为向量的长度实际是由电路的配置决定的。但我们并不希望在证明中将向量的长度进行编码,因为电路在运行时是固定大小的,证明也是。- 很容易误将一些不属于协议 transcript 的数据放到
Proof结构体里,这对 proving system 的实现会是一个潜在的风险。 - 我们需要同时创建多个 PLONK 证明,而这些证明虽然是给同一个电路的,但它们共享许多不同的子结构体。
因此, halo2 将证明数据视作透明的字节流。这些字节流通过 transcript 创建和消费:
TranscriptWritetrait 代表某些我们可以在证明期写入的数据TranscriptReadtrait 代表某些我们可以在验证期读取的数据
重要的是, TranscriptWrite 的实现需要满足同时向某个 std::io::Write 缓冲写入的能力,这点对于 TranscriptRead 和 std::io::Read 也是一样。
另外,将证明作为透明字节流对待能让验证过程关注优化反序列化,在进行点的压缩时这一开销是不能忽视的。
证明的编码
在曲线 上的 Halo2 证明被编码为一些点和标量的字节流:
- 点 ) 用于表示多项式的承诺
- 标量 ) 用于表示多项式在某个点的取值,以及盲因子等
对于 Pallas 和 Vesta 两条曲线来说,点和标量都用32字节进行编码,因此最后的证明总是32字节的整数倍。
halo2 包支持同时证明一个电路的多个 instance ,这样可以共享一些常用的证明组件和协议逻辑。
我们使用如下的电路常量以描述证明的编码:
- - 电路的大小( 行)
- - advice 列的数量
- - fixed 列的数量
- - instance 列的数量
- - lookup argument 的数量
- - permutation argument 的数量
- - 在 permutation argument 中用到的列的数量
- - 商数多项式的最大度数
- - advice column 的询问数
- - fixed column 的询问数
- - instance column 的询问数
- - 可以同时证明的电路 instance 数量
因为证明的编码是直接根据 transcript 进行的,我们可以将其按 Halo 2 协议划分成几个部分:
-
PLONK 承诺 :
- 个点(重复 次)
- 个点(重复 次)
- 个点(重复 次)
- 个点(重复 次)
-
Vanishing argument :
- 个点.
- 个标量(重复 次)
- 个标量(重复 次)
- 个标量
- 个标量
-
PLONK 求值:
- 个标量(重复 次)
- 个标量(重复 次)
-
多点打开证明:
- 1 个点.
- 在证明中的每个点集对应 1 个标量
-
多项式承诺方案:
- 个点.
- 个标量.
域
halo2 中使用的 Pasta曲线 是两条在有限域上均有阶为 的大乘法子群的曲线。这意味着我们可以将有限域的阶写为 ,其中 为奇数。对于 Pallas 和 Vesta 曲线,我们都有 。
Sarkar 平方根算法(基于查表的变式)
在 halo2 中,我们使用 Sarkar2020 论文中的技术计算平方根。该算法的思想是,我们可以将计算平方根的任务在每个乘法子群中进行拆分。
假设我们想要求 模某个 Pasta 素数阶 的平方根,( 是 上的一个非零完全平方数),我们可以定义一个 阶的 单位根 ,( 是 中的非平方数),并计算如下辅助表格:
令 。我们可以定义 作为 阶乘法子群上的一个元素。
令
当 i = 0, 1 时
使用 表,我们查找 使得
定义
当 i = 2 时
查找 使得
定义
当 i = 3 时
查找 使得
定义
最终结果
查找 使得
令 .
我们写成
将等式右边进行平方,我们得到 。因此, 的平方即为 ;第一个部分在之前已有计算,第二部分可以通过在 中查表并计算得到。
组件
在这一章节,我们记录一些 Halo 2 中常用 gadget 和 chip 的设计样例。
注意:这些 gadget 和它们的实现方式都没有经过 review ,不应用于生产环境中。
SHA-256
规范
SHA-256 在 NIST FIPS PUB 180-4 有过规范的定义。
和上述规范定义不同的是,这里我们使用 表示和 的加模运算 ,用 表示域上的加法。 用于表示异或。
组件(gadget)接口
SHA-256 使用8个32位的变量维护一个内部状态。SHA-256算法使用512比特位为一个区块作为输入,在算法内部将这些区块分解成32位的一些 chunk 。因此我们将SHA-256的组件设计为每次使用32位的 chunk 作为其输入。
芯片(chip)指令
SHA-256 gadget 要求芯片具有如下的指令:
#![allow(unused)] fn main() { extern crate halo2; use halo2::plonk::Error; use std::fmt; trait Chip: Sized {} trait Layouter<C: Chip> {} const BLOCK_SIZE: usize = 16; const DIGEST_SIZE: usize = 8; pub trait Sha256Instructions: Chip { /// Variable representing the SHA-256 internal state. type State: Clone + fmt::Debug; /// Variable representing a 32-bit word of the input block to the SHA-256 compression /// function. type BlockWord: Copy + fmt::Debug; /// Places the SHA-256 IV in the circuit, returning the initial state variable. fn initialization_vector(layouter: &mut impl Layouter<Self>) -> Result<Self::State, Error>; /// Starting from the given initial state, processes a block of input and returns the /// final state. fn compress( layouter: &mut impl Layouter<Self>, initial_state: &Self::State, input: [Self::BlockWord; BLOCK_SIZE], ) -> Result<Self::State, Error>; /// Converts the given state into a message digest. fn digest( layouter: &mut impl Layouter<Self>, state: &Self::State, ) -> Result<[Self::BlockWord; DIGEST_SIZE], Error>; } }
TODO: Add instruction for computing padding.
这些指令的选择考虑到了可复用性和可优化空间的平衡。我们考虑将 compression 函数分割成几个组成部分,然后提供一个实现了不同轮次逻辑的 compression 组件。但是这会使得芯片无法使用同在一个 compression 轮次的不同部分的相对位置引用。使用一条指令实现所有的 compression 轮次非常类似于 Intel 的 SHA 指令集扩展,后者也是提供了一条指令对应多个 compression 轮次。
SHA-256 的 16位表芯片(chip)
该芯片是基于一个16位查找表实现的,电路需要最小 行,适于整合进一些大的电路中。
我们的目标是使约束的度数最大为9。这让我们能够在同一行内处理进位的约束,以及对一些 的小片约束。
Compression 轮次
总共有64个 compression 轮次。每轮使用8个32位数 作为输入,然后执行如下操作:
需要处理进位 的情况。
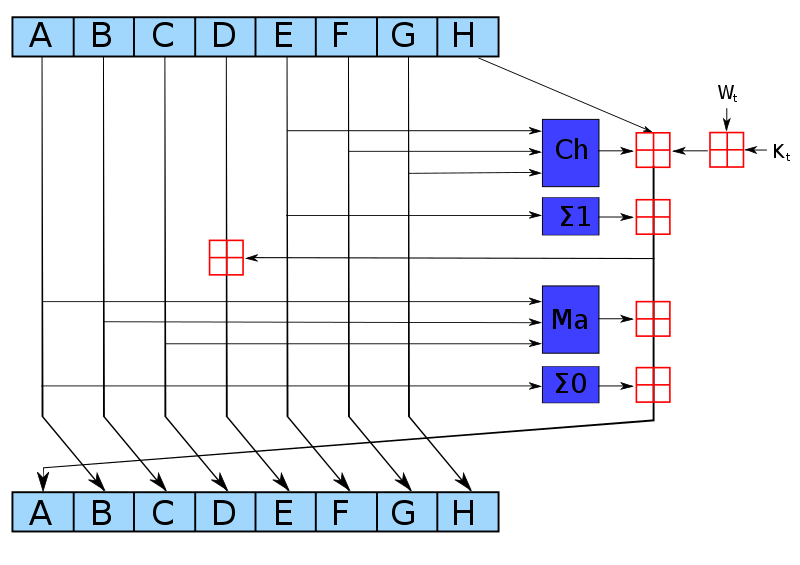
定义 为一个16位的输入-输出映射表。我们不需要另外定义映射表来进行范围约束,可以通过复用 实现该功能。
模加操作
我们注意到模 的加法,和先在有限域上做加法,然后通过掩码取出低32位的操作是等价的。例如,有两个操作数 和 :
我们将操作数分解为16位一个的 chunks :
然后使用有限域的加法重新定义约束:
更一般化的,输出可以被分解为任意的比特位组合,而不仅仅是16位一组的 chunks 。注意上述等式已经正确处理了从 的进位。
约束要求每个 chunk 都是在正确范围内的,否则之后的赋值可能会导致有限域上的溢出。
-
操作数和结果的 chunk 可以通过 约束,具体方法是在表格的某个子集中的 "dense" 列中查找其 chunk 是否存在。我们通过这种方式还能获得输出结果的 "spread" 形式。特别是对于右下角的 其输出将变为 ,左下角的 其输出将变为 。我们在后面对 和 的优化中将用到它。
-
必须被约束为操作数数量所允许的进位值的一个精确范围。我们通过 small range constraint 来进行约束。
Maj 函数
可以通过 次查找完成: chunks
- 正如之前提到的,在第一轮之后我们已经有了了 的 spread 形式 。类似的, 和 相当于上一轮次中的 和 ,因此在稳态中我们也已有了它们的 spread 形式 和 。实际上,我们也可以假设我们在第一轮就有了它们的 spread 形式,要么从 fixed IV 或者从上一个块对 的使用中获取。
- 在域中添加 spread 形式:
- 我们可以以 32位计算机字的形式或者以片(piece) 的形式添加,两者是等价的
- 对于 ,分别计算偶数位 和奇数位 。
- 将 约束为 ,其中 为 函数的输出output。
注意:“偶数位”指的是 的偶数次方的权重,同理,“奇数位”我们指 的奇数次方的权重
Ch 函数
TODO: can probably be optimized to or lookups using an additional table.
可以通过 次查找完成: chunks
- 如之前所提到的,在第一轮之后我们已经有了 的 spread 形式 。类似的,我们有 和 和上一轮中的 和 相等,因此在稳态中我们已经有了 和 的 spread 形式。实际上,我们也可以假设我们在第一轮中已经有了它们的 spread 形式,要么从 fixed IV 或者从上一个块对 的使用中获取。
- 计算 和 ,其中 。
- 我们可以以 32位计算机字的形式或者以片(piece)的形式添加,两者是等价的
- 用于计算 的 spread ,尽管取反操作和 一般不满足交换律。可以这样计算是因为 中的每个 spread 位都减去了 ,因此没有借位。
- 计算 使得 ,对 也有类似的计算。
- 即为 函数的输出。
Σ_0 函数
可以通过 次查找完成。
我们首先将 分成长度为 的片 ,以小数端为例。同时我们也取出这些片的 spread 形式。这可以在 PLONK 电路中的两行内完成,因为10位的片和11位的片可以使用 的查找获得,而9位的片可以被进一步分为3个3位的子片。后者和剩下的2位的片可以通过多项式约束来限制它们的取值范围,每行两个片。这些小的片的 spread 形式可以由插值构成。
注意到将 chunk 划分为片可以和 的规约一起做,即后者不需要额外的查找了。在最后一轮,我们将 在前馈加法(需要最多处理7次进位)做完后进行规约。
等价于 :
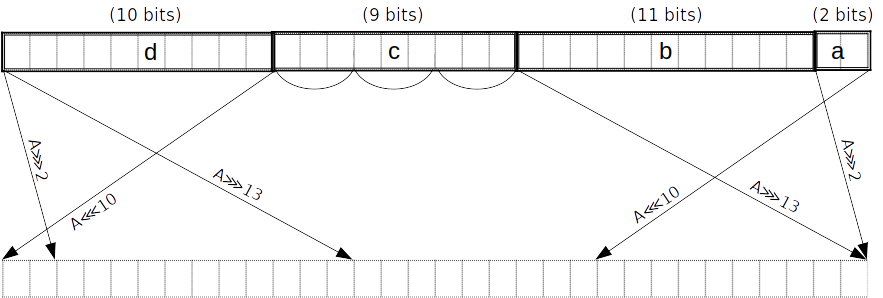
然后,使用 个额外的 查找,我们可以得到结果 ,其二进制偶数位是上面片的一个线性组合。
即,我们计算出压缩后的偶数位 和压缩后的奇数位 ,并约束
其中 就是 函数的输出。
Σ_1 函数
可以通过 次查找完成。
我们首先将 分成长度为 的片 ,以小数端为例。同时我们也取出这些片的 spread 形式。这可以在 PLONK 电路中的两行内完成,因为7位的片和14位的片可以使用 的查找获得,5位的片可以被进一步分为3位3位的子片,6位的片可以被分解为2个3位的片。这4个小的片可以通过多项式约束来限制它们的取值范围,每行两个片。这些小片的 spread 形式可以由插值构成。
注意到将 chunk 划分为片可以和 的规约一起做,即后者不需要额外的查找了。在最后一轮,我们将 在前馈加法(需要最多处理7次进位)做完后进行规约。
等价于 .
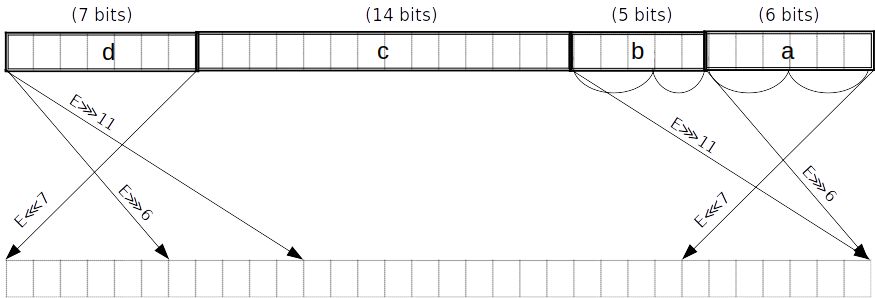
然后,使用 个额外的 查找,我们可以得到结果 ,其二进制偶数位是上面片的一个线性组合。
即,我们计算出压缩后的偶数位 和压缩后的奇数位 ,并约束
其中 就是 函数的输出。
块分解
对于消息中每一个512位的块 来说,其 个 位的计算机字可以通过以下方式构造:
- 前 个字可以通过将 分解为32位的块来获得
- 剩下的 个字通过如下公式构造: for .
Note: 的下标从 开始
Note: 是右移位运算,不是循环,和 区分
σ_0 函数
等价于 。

和之前类似,也用小数端表示,但 的长度分别为 。将 分解为两个2位的子片。
σ_1 函数
is equivalent to .
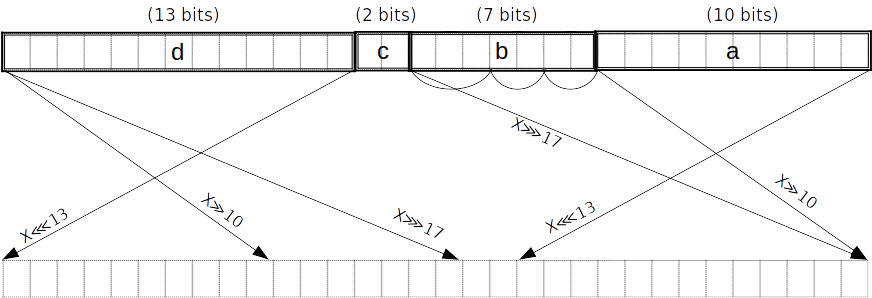
TODO: this diagram doesn't match the expression on the right. This is just for consistency with the other diagrams.
和之前一样用小数端表示, 的长度分别为 。将 分解为 位的子片。
消息调度
我们将 应用于 ,将 应用于 。为避免重复的应用 ,我们可以将 的分解进行合并。合并长度为 和 的片会得到长度分别为 的片。
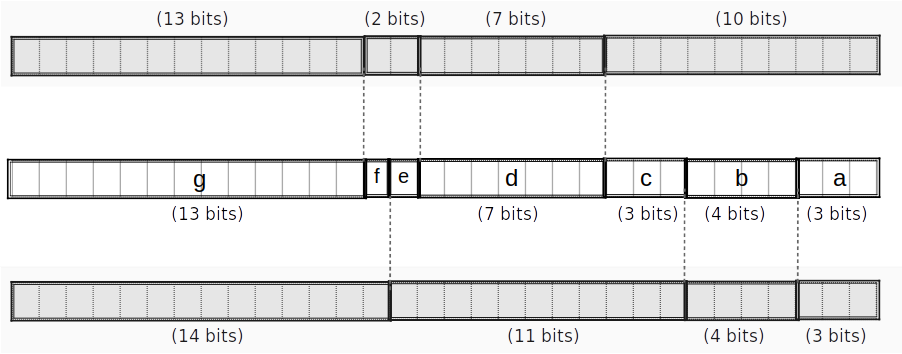
如果我们可以将合并后的分解在3行中完成(单独分解 和 需要4行),我们就能节省下35行。
These might even be doable in rows; not sure. —Daira
我们可以将 模 的规约合并至它们在后续计算中的分解时,类似于我们对 和 做过的操作。
我们仍然需要对 进行规约,因为它们没有被分解。(技术上,我们可以暂时不对它们做规约,在后面计算 和 的时候会做规约,但是这会导致我们需要处理多达10次进位,而不是现在的6次,因此还是值得的)。
优化后的调度结果为:
- 行用来约束 至 比特位
- 技术上这不是必须的,这里进行约束是保持鲁棒性,因为输入部分的约束是免费的
- 行用来拆分 为4个 比特位的 pieces
- 行用来拆分 为 比特位的 pieces (和 的规约进行合并)
- 行用来拆分 为 比特位的 pieces (和规约进行合并)
- 行用来提取 的 计算结果
- 行用来提取 的 计算结果
- 行用来规约
- rows.
总开销
对每一轮次:
- 行
- 行
- 行
- 行
- 和 是无开销的
- 每轮行数
这里第三步总计 行,再加上:
- 行(进行消息调度之后)
- 行给第4步中进行的8次模 的规约
总共是 行。
表格
我们只需要一个有 行 列的 表。我们需要一个标签列,用以将 and 表格的 比特位子集挑选出来。
spread 表格
| 行 | 标签 | 表格 (16位) | spread (32位) |
|---|---|---|---|
| 0 | 0000000000000000 | 00000000000000000000000000000000 | |
| 0 | 0000000000000001 | 00000000000000000000000000000001 | |
| 0 | 0000000000000010 | 00000000000000000000000000000100 | |
| 0 | 0000000000000011 | 00000000000000000000000000000101 | |
| ... | 0 | ... | ... |
| 0 | 0000000001111111 | 00000000000000000001010101010101 | |
| 1 | 0000000010000000 | 00000000000000000100000000000000 | |
| ... | 1 | ... | ... |
| 1 | 0000001111111111 | 00000000000001010101010101010101 | |
| ... | 2 | ... | ... |
| 2 | 0000011111111111 | 00000000010101010101010101010101 | |
| ... | 3 | ... | ... |
| 3 | 0001111111111111 | 00000001010101010101010101010101 | |
| ... | 4 | ... | ... |
| 4 | 0011111111111111 | 00000101010101010101010101010101 | |
| ... | 5 | ... | ... |
| 5 | 1111111111111111 | 01010101010101010101010101010101 |
例如,如果要做一次 个比特位的 查表,我们先对标签进行多项式约束使其必须为 。在最常用的 位查表中,我们不需要约束标签列。注意我们可以在没有用到的行中(即超过 的行数)填充任意重复值,例如都填充为全零行。
门
Ch 门
从之前操作来的输入:
- 是 32位字 的 位 spread 形式,假设服从之前的约束
- 实际中,我们在分解 为 位子片后能得到 的 spread 形式
- 定义为
E ∧ F
| s_ch | |||||
|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | ||||
| 1 | {0,1,2,3,4,5} | ||||
| 0 | {0,1,2,3,4,5} | ||||
| 0 | {0,1,2,3,4,5} |
¬E ∧ G
| s_ch_neg | ||||||
|---|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | |||||
| 1 | {0,1,2,3,4,5} | |||||
| 0 | {0,1,2,3,4,5} | |||||
| 0 | {0,1,2,3,4,5} |
约束:
s_ch(choice):s_ch_neg(negation): 检查s_ch是否为负数- 在 中查找
- 之间的置换
输出:
Maj 门
从之前操作来的输入:
- 32位字的 的 位 spread 形式 ,假设服从之前的约束
- 实际中,我们在分解 为 位子片后能得到 的 spread 形式
| s_maj | ||||||
|---|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | |||||
| 1 | {0,1,2,3,4,5} | |||||
| 0 | {0,1,2,3,4,5} | |||||
| 0 | {0,1,2,3,4,5} |
约束:
s_maj(majority):- 在 中查找
- 之间的置换
输出:
Σ_0 门
是一个 32位字,分解为 位 chunks,从小数端开始。我们将这些 chunks 分别称为 ,并且进一步将 分解为3位的 chunks 。我们将小 chunks 的 spread 形式写成 witness :
| s_upp_sigma_0 | |||||||
|---|---|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | ||||||
| 1 | {0,1,2,3,4,5} | ||||||
| 0 | {0,1,2,3,4,5} | ||||||
| 0 | {0,1,2,3,4,5} |
约束:
s_upp_sigma_0( 约束):
- 在 中查找
- 中的 2比特位范围检查及2比特位 spread 检查
- 上的 3比特位范围检查和3比特位 spread 检查
(见 辅助门)
输出:
Σ_1 门
是一个 32位字,分解为 位 chunks,从小数端开始。我们将这些 chunks 分别称为 ,并且进一步将 分解为两个3位的 chunks ,并更进一步将两个3比特位的chunk 和 分解为 (2,3)比特位的 chunks 。我们将小 chunks 的 spread 形式写成 witness :
| s_upp_sigma_1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | |||||||
| 1 | {0,1,2,3,4,5} | |||||||
| 0 | {0,1,2,3,4,5} | |||||||
| 0 | {0,1,2,3,4,5} |
约束:
s_upp_sigma_1( constraint):
- 在 中查找
- 中的 2比特位范围检查及2比特位 spread 检查
- 上的 3比特位范围检查和3比特位 spread 检查
(见辅助门)
输出:
σ_0 门
v1
门的v1占一个字,可以分解为 位的 chunks (已经在消息调度中被约束)。我们将这些 chunks 称为 被进一步分解为两个2比特位的 chunks 我们将小 chunks 的 spread 形式写成 witness 。我们从消息调度中已经获得了 和 。
等价于 。
| s_low_sigma_0 | |||||||
|---|---|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | ||||||
| 1 | {0,1,2,3,4,5} | ||||||
| 0 | {0,1,2,3,4,5} | ||||||
| 0 | {0,1,2,3,4,5} |
约束:
s_low_sigma_0( v1 约束):
- 检查
b是否被正确的分解为4比特位的一些片 - 中的 2比特位范围检查及2比特位 spread 检查
- 上的 3比特位范围检查和3比特位 spread 检查
v2
门的v2占一个字,可以分解为 位的 chunks (已经在消息调度中被约束)。我们将这些 chunks 称为 我们从消息调度中已经获得了 和 。1比特位的 在 spread 操作中不做更改,可以直接使用。另外 被进一步分解为两个2比特位的 chunks 我们将小 chunks 的 spread 形式写成 witness 。
等价于 。
| s_low_sigma_0_v2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | |||||||
| 1 | {0,1,2,3,4,5} | |||||||
| 0 | {0,1,2,3,4,5} | |||||||
| 0 | {0,1,2,3,4,5} |
约束:
s_low_sigma_0_v2( v2 约束):
- 检查
b是否被正确的分解为4比特位的片 - 中的 2比特位范围检查及2比特位 spread 检查
- 上的 3比特位范围检查和3比特位 spread 检查
σ_1 门
v1
门的v1占一个字,可以分解为 位的 chunks (已经在消息调度中被约束)。我们将这些 chunks 称为 被进一步分解为 比特位的 chunks 我们将小 chunks 的 spread 形式写成 witness 。我们从消息调度中已经获得了 和 。
等价于 .
| s_low_sigma_1 | |||||||
|---|---|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | ||||||
| 1 | {0,1,2,3,4,5} | ||||||
| 0 | {0,1,2,3,4,5} | ||||||
| 0 | {0,1,2,3,4,5} |
约束:
-
s_low_sigma_1( v1 约束): -
检查
b是否被正确的分解为7比特位的片。 -
中的 2比特位范围检查及2比特位 spread 检查
-
上的 3比特位范围检查和3比特位 spread 检查
v2
门的v2占一个字,可以分解为 位的 chunks (已经在消息调度中被约束)。我们将这些 chunks 称为 我们从消息调度中已经获得了 和 。1比特位的 在 spread 操作中不做更改,可以直接使用。另外 被进一步分解为两个2比特位的 chunks 我们将小 chunks 的 spread 形式写成 witness 。
等价于 。
| s_low_sigma_1_v2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | {0,1,2,3,4,5} | |||||||
| 1 | {0,1,2,3,4,5} | |||||||
| 0 | {0,1,2,3,4,5} | |||||||
| 0 | {0,1,2,3,4,5} |
约束:
s_low_sigma_1_v2( v2 constraint):
- 检查
b是否被正确的分解为4比特位的子片。 - 中的 2比特位范围检查及2比特位 spread 检查
- 上的 3比特位范围检查和3比特位 spread 检查
辅助门
小范围约束
令 . 约束该表达式的值为0,相当于约束了
2比特位范围检查
| sr2 | |
|---|---|
| 1 | a |
2比特位 spread
| ss2 | ||
|---|---|---|
| 1 | a | a' |
插值多项式:
- ()
- ()
- ()
- ()
3比特位范围检查
| sr3 | |
|---|---|
| 1 | a |
3比特位 spread
| ss3 | ||
|---|---|---|
| 1 | a | a' |
插值多项式:
- ()
- ()
- ()
- ()
- ()
- ()
- ()
- ()
reduce_6 门
6元素的 加法
输入:
检查:
假设输入被约束为16个比特位
- 加法门 (sa):
- 进位门 (sc):
| sa | sc | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | ||||||||
| 1 | 1 |
假设输入被约束为16个比特位
- 加法门 (sa):
- 进位门 (sc):
| sa | sc | ||||
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 1 | 1 | ||||
| 0 | 0 | ||||
| 1 | 0 |
reduce_7 门
7元素的 加法
输入:
检查:
假设输入被约束为16个比特位
- 加法门 (sa):
- 进位门 (sc):
| sa | sc | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | |||||||||
| 1 | 1 |
消息调度区域
对于消息 中的每一个 block ,其64个32位字以如下方式构造:
- 通过将 以每32个比特进行划分,得到前16个
- 剩下的48个字使用如下的方式构造:
for .
| sw | sd0 | sd1 | sd2 | sd3 | ss0 | ss0_v2 | ss1 | ss1_v2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4} | |||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| .. | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3} | |||||||||
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| .. | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | {0,1,2,3} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| .. | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} |
约束:
sw: 使用 构造字sd0: 对应的分解门sd1: 的分解门 (分解为 位的片)sd2: 的分解门 (分解为 位的片)sd3: 的分解门 (分解为 位的片)
Compression 区域
+----------------------------------------------------------+
| |
| 分解 E, |
| Σ_1(E) |
| |
| +---------------------------------------+
| | |
| | reduce_5() 以获得 H' |
| | |
+----------------------------------------------------------+
| 分解 F, 分解 G |
| |
| Ch(E,F,G) |
| |
+----------------------------------------------------------+
| |
| 分解 A, |
| Σ_0(A) |
| |
| |
| +---------------------------------------+
| | |
| | 使用 H' 和 reduce_7(), |
| | 以获得 A_new |
| | |
+------------------+---------------------------------------+
| 分解 B, 分解 C |
| |
| Maj(A,B,C) |
| |
| +---------------------------------------+
| | 使用 H' 和 reduce_6(), |
| | 以获得 E_new |
| | |
+------------------+---------------------------------------+
初始轮:
| s_digest | sd_abcd | sd_efgh | ss0 | ss1 | s_maj | s_ch_neg | s_ch | s_a_new | s_e_new | s_h_prime | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} |
稳态
| s_digest | sd_abcd | sd_efgh | ss0 | ss1 | s_maj | s_ch_neg | s_ch | s_a_new | s_e_new | s_h_prime | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | {0,1,2,3,4,5} |
最后的摘要输出:
| s_digest | sd_abcd | sd_efgh | ss0 | ss1 | s_maj | s_ch_neg | s_ch | s_a_new | s_e_new | s_h_prime | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
背景资料
该部分包含了理解Halo 2证明系统所必须的背景资料。该部分面向的是ELI15水平(即读者只需15岁知识水平);如果您想进一步提供补充材料,联系我们!
域
对于众多密码学协议来说,域 —— 一种代数结构,都是一个最基本的组件。域,就是指拥有 和 两个二元运算的集合(通常是数集),并且满足一系列 域公理。举例来说,实数集 就是一个拥有不可数无穷多元素的域。
Halo运用有限域,所谓有限域是指域的元素个数是有限的。有限域完全分类如下:
-
如果 是有限域,那么它包含 个元素,其中 是整数且 , 是一个素数。
-
任意两个有相同元素个数的有限域是同构的。特别的,素域 上的算术运算与整数模 上的加法和乘法是同构的,也就是说,。这就是我们将 作为 模数 的原因。
我们定义一个域 其中 . 素数 称为它的 特征。 如果 , 那么域 就是域 的 阶扩张。 (相类似,复数 就是实数域的扩张)。但是, 在Halo中,我们并不使用扩域。当我们写 我们指的是拥有素数 个元素的 素域,也就是说此时 。
重要注释:
-
任何域中,都有两个特殊的元素: ,加法的单位元; ,乘法的单位元。
-
一个域中的元素,其在二进制表示中的最低位,可以用来代表它在域上的“符号”以区分它的加法逆元(即负数)。这是因为,对任意一个最低位为 的非零元素 其加法逆元 的最低位一定是 ,反之亦然。我们也可以用一个元素是不是大于 来作为其“符号”。
有限域对于后文中构建 多项式 和 椭圆曲线 是很有用处的。 椭圆曲线是一个群,我们将马上对群展开讨论。
群
与域相比,群更加简单,并且更多限制;群只有一个二元运算 ,和更少的公理。群也有一个单位元,我们用 表示。
群中任意一个非零元素 必有一个 唯一 的 逆元,记为 ,满足 。
举个例子,域 中所有非零元素形成一个群,同时定义该群的运算就是域上的乘法。
(备注) 加法 vs 乘法符号
如果将 写做 或是干脆不写 (比如: 将 写做 ), 那么正如上文所述,单位元 就写做 , 它的逆元就是 ,我们说这样的群“被写作乘”。而如果将 视为 , 那么它的单位元就是 或者 , 它的逆元就是 , 我们说这样的群“被写做加”。 通常,椭圆曲线群用加法符号来表示, 而对于有限域中的元素构成的群用乘法符号表示
当我们使用加法符号时,将写如下式子:
对于任意非负 我们称上式为“标量乘法”;通常,我们使用大写字母变量来表示群的元素。当我们使用乘法符号时,如下等式
就被称为“指数”。无论上述那种情况,我们都将满足 或 的 称为 在基 下的“离散对数”。 我们可以通过求逆运算 将标量扩展到其逆,也就是说: 或者 .
有限域元素 的 阶 定义为满足如下条件的最小的正整数 , (乘法符号)或者 (加法表示)。 群的阶 就是指群包含的元素的个数。
群总有一个 生成集,所谓生成集是这样一个集合,可以使用该集合中的元素通过这些元素的乘方运算(乘法术语)来生成群中的任意一个元素。 如果,生成集是 , 我们就可以通过 生成群的所有元素。对于一个给定的群,它有很多不同的生成集。
如果一个群的存在一个生成集(不一定是唯一的)只有一个元素,记为 ,那么这个群就是一个循环群。进而,我们称 生成了这个群,并且 的阶就是该群的阶。
任意一个阶为 的有限循环群 与整数modulo (记为 )是同构的,满足:
- 上的运算 与modulo 的加法对应;
- 的单位元与 对应;
- 有一个生成元 与 对应.
对于一个给定的生成元 ,容易证明 是成立的,因为(或是用加法符号, )。通常,证明 会难一些。我们将在椭圆曲线中进一步讨论这个问题。
如果一个有限群的阶 是一个素数,那么该群是个循环群,并且每个非单位元元素都是其生成元。
有限域的乘法子群
我们用符号 来代表集合 上的乘法群(也就是说,群的运算就是 的乘法)。
在子群,一个快速求逆的方法是 。这是因为,由费马小定理可知,如果 是一个素数, 对任意整数 且 不是 的倍数,都有 。如果 是非零整数,那么我们可以除两次 就获得 。
设 是 的生成元,所以 的阶是 (等于 的元素的个数). 因此,对任意一个 都存在唯一一个 满足 .
值得注意的是 其中 确实可以表示成 其中 并且 。实际上,对任意 它也保持了如下运算 。因此,域上非零元素的乘法就可以表示成关于某个特定生成元 的在 模 上的加法。这个加法,就出现在“指数”上。
这是另一种理解 就是域元素的逆元的方法:
所以 。
蒙哥马利技巧
蒙哥马利技巧,以彼得 · 蒙哥马利 (RIP) 得名,是同时计算很多群元素的逆元的一种方法。 它通常用于在 中求逆,在其上求逆运算 要比乘法运算代价大得多。
假设我们要计算三个非零元素 的逆元。不似常规,我们将计算如下两个积 和 ,并且计算如下的逆
现在我们可以 乘以 以获得 ,并且 乘以 得到 , 进一步该值分别乘以 就分别获得了想要的逆元。
该技术可以推广,仅仅一次求逆运算就可以计算出任意个数的群元素的逆。
乘法子群
所谓群 在 下的 子群 就是, 中元素的一个子集在 下仍然是一个群。
在前面的章节中,我们说 是 -阶群 的生成元。 该群拥有 合数 阶,所以依据中国剩余定理1 它有真子群。举个例子,假设 ,那么 可以分解为 。因此,存在一个 以 为生成元的 -阶子群和一个以 为生成元的 -阶子群。进一步, 中所有元素都可以表示为 其中 (modulo ) 和 (modulo ).
如果我们有 请注意如下计算过程
我们“消灭”了 -阶子群部分,仅仅只用 -阶子群就生成了这个值。
拉格朗日定理 (群论) 告诉我们,有限群 的任意一个子群 的阶能整除 的阶。因此 的任何子群的阶必定能整除 。
PLONK-based 证明系统, 如 Halo 2,可以更方便的利用拥有大量乘法子群的域,并且这些子群是“平滑”分布(好处是使得性能差距更小,并且可以以更细的力度增长电路规模)。Pallas 和 Vesta 曲线有如下形式的素数
其中 并且 奇数 (这就是说, 的低32位都是 )。这意味着,它们有阶为 的乘法子群,其中 。这些 2进制乘法子群对efficient FFTs 十分友好,而且也可以支持多种电路规模。
平方根
在域 有一半的非零元素都是完全平方元素;剩下的就是非平方或者“二次非剩余”。为了说明此一事实,考虑 生成的 的 2-阶乘法子群(该子群必然存在,因为当 是一个大于等于 的素数的时候, 能被 整除)和一个由 生成的 的 -阶乘法子群,其中 。进而每个元素 均可以唯一地表示为 其中 并且 。那么有一半的元素满足 而另一半元素满足 。
考虑一个简单的例子, 那么 必是一个奇数 (如果 是偶数,则 必能被 整除,而这与 是 矛盾)。 如果 是一个完全平方数,则必存在一个 使得 。这就意味着,
换句话说,某个特定域中的完全平方数不可能生成其 -阶乘法子群,而且由于有一半的元素可以产生其 -阶子群,所以该域中至多有一半的元素是完全平方数。事实上,有且仅有一半的元素是完全平方数(这是因为,每一个非平方元素的平方都是唯一的)。这就意味着,我们可以假设所有的完全平方数都可以表示为 对某个 ,因此求平方根就变成了一个指数运算,指数就是 。
而如果 那问题就变得复杂得多,因为 并不存在。 记 = 其中 是奇数。不可能,上面已经讨论,现在考虑 。 生成一个 -阶乘法子群而 生成一个奇数 -阶得乘法子群。 进而每个元素 都可以表示为 其中 并且 。如果某元素是完全平方数,就是说存在 而 本身可以表示为 对于 和 。这意味着 , 因此我们推出 ,并且 。那么在这种情况下 就必须是一个偶数,否则对任意 , 就不能成立。反之,如果 不是一个完全平方数,那么 就是一个奇数。综上,一半的元素是完全平方数。
为了计算平方根,我们首先将 升次到 以“消灭” -阶部分,计算
然后在此基础上计算 次方,以消除其 -阶部分原始指数的影响:
(因为 与 是互素的)。这就暴露出 的值可以让我们进一步处理。 相似的,我们可以消除 -阶部分以获得 (译者注:此处应该是笔误,),将这两个值合起来就得出了平方根。
已经证明当 时,有更简便的方法来合并这些指数以提高效率。 而对于其他的 值,唯一获取 的方法就是,不断平方以最终确定 的每一位。 这就是 Tonelli-Shanks square root algorithm 算法的本质,并且该算法还描述了一半的策略。 (当然还有另外一种用二次扩域的求取平方根的算法,但是直到素数变得相当大时,该算法才有效率优势)。
单位根
在前一章节,我们令 其中 是奇数,并且阐明 元素 生成其 -阶子群。 为方便起见,不妨设 。那么元素 都被称为 次 单位根。
所谓 本原单位根,,是满足如下条件的 次单位根 除非 .
重要补充:
-
如果 是一个 次单位根,那么 满足 。如果 ,那么 。
-
相应地,单位根集合就是如下方程的解
-
("负数引理")。证明: 因为 的阶是 , 。因此,。
-
("折半引理")。证明:
换句话说,如果我们平方每一个 次单位根集合中的元素,我们只会得到一半的元素 (这就是 次单位根)。 在元素和它们的平方之间存在一个 的映射。参考
多项式
是一个以 为自变量的 上的多项式。例如,
就定义了一个 次多项式。 是常数项。 次多项式有 个系数。 我们经常想要将自变量 用一个具体值 替换掉,以计算其在该具体值 处的值,表示为 。
在数学上这通常被称为 “求 在点 处的值”。 所谓“点”,是从多项式的几何表示来的, 将多项式表示为 ,那么 就是一个二维空间中的一个点的坐标。 但是我们处理的多项式通常总是等于零,并且 是一个某个域中的元素。 不应该与椭圆曲线的点混淆,椭圆曲线上的点的说法我们也要经常使用,但是不在多项式求值的语境下使用。
重要说明:
-
多项式相乘,将产生这样一个积多项式,该多项式的次数是其因子多项式的次数的和。多项式除法,则会减去相应的次数。
-
给定一个 次多项式 ,如果我们在 个不同点求取了多项式的值,那么这些值就能唯一确定该多项式。 换句话说,给定 个不同点值,我们就能通过多项式插值来唯一确定 次多项式 。
-
是多项式 的 系数表示, 我们也可以用它在 个不同点处的 点值表示 来表示它。不管那种表示方法,都唯一确定了相同的多项式。
(备注) 霍纳法则
霍纳法则可以仅仅使用 次乘法和 次加法就高效地求得一个 次多项式在某处的取值。 霍纳法则如下:
快速傅里叶变换 (FFT)
FFT是一种在系数表示和点值表示之间进行转换的高效方法。它在多项式的 个 次单位根上求取多项式的值。 这 个 次单位根是 其中 是多项式的主单位根。 通过利用单位根中的对称性,FFT的每一轮计算都只计算问题规模的一半。绝大多数情况下,我们都要求多项式的次数是 的 幂次,即 ,并递归运用减半算法。
动机:快速计算多项式乘法
在系数表示下,计算多项式相乘需要 次计算。 比如,:
显而易见,第一个多项式中的 项必须与第二个多项式的 项相乘。
而在点值表示下,多项式相乘仅仅需要 计算:
每个值都按照点的顺序相应计算即可。
这就提示了如下的快速计算多项式乘法的策略:
-
对多项式在 个点处求值(转成点值表示)
-
在点值表示下,按照点的顺序依次计算积多项式的点 () (计算积多项式的点值表示);
-
将积多项式的点值表示转换成系数表示。
现在的挑战就是如何高效地进行多项式 求值 和 插值。 最朴素的方法,对多项式在 个点处进行求值将需要 计算(我们在每一个点处都使用 的霍纳法则):
方便起见,我们将如下表示上面的矩阵:
( 就是 的 离散傅里叶变换; 也被称为 范德蒙矩阵。)
(radix-2) Cooley-Tukey 算法
我们的策略就是将一个规模为 的 DFT 分成两个规模分别为 的 DFT。假定多项式 我们将其按照奇数项和偶数项进行拆分:
于是原多项式就是:
尝试在 and , 处求值,我们就能发现某些对称性:
值得注意的是,我们仅仅在一半的domain上求取 和 这是因为 (折半引理)。
但是这些值却能帮助我们在完整domain 上求出 。 这就意味着,我们将一个成都为 的 DFT 转化成了两个长度为 的 DFT。
我们选择 为 的幂次(必要时,可以添 补齐),然后递归地运用这种分治策略。 由主定理可知1,这种多项式求值算法仅需要 计算,这就是著名的快速傅里叶变换(FFT)。
逆FFT
我们已经求得了多项式的值并将它们按照点的顺序进行了相乘。剩下的工作就是要把积的点值表示转换成系数表示。 做这件事,我们仍然是在点值上调用FFT。只不过,这次我们将做如下修正:
- 将范德蒙矩阵中的 用 替换掉
- 把最后的结果乘以 。
也就是:
(为了理解为什么逆FFT与FFT有相似的形式,请参考 13-1 2。下图也是从 2来的。)

Schwartz-Zippel 引理
Schwartz-Zippel 引理的通俗解释就是 “不同的多项式在绝大多数点上的值都是不同的”。 它的正式表述如下:
令 是有 个变量的 次非零多项式。 是一个至少有 个元素的集合。如果我们从 中随机选择 ,
在 是我们更熟悉的单变量多项式的情况下,如 退化成,一个 次的非零多项式至多有 个根。
Schwartz-Zippel引理可以用来检验两个多项式是否相等。设有两个多变量的多项式 和 ,它们的次数分别是 。 我们选取随机数 ,其中 的元素个数至少是 , 进而验证 是否都成立。 如果两个多项式相同,那么上式会一直成立,而如果两个多项式不相同,那么上式成立的概率至多就是 。
Vanishing多项式
考虑这样一个 -阶乘法子群 ,它的主单位根是 。 对所有 ,有 。这就是说 中的每个元素都满足如下等式
这就是说每个元素都是 的根。我们称 就是在 上的 Vanishing 多项式 因为该多项式在 中每个元素处的取值都为 。
这在检验多项式约束的时候尤其有用。举个例子, 检验 在 上的正确性,我们只需简单地验证 的 倍数。这就是说,如果我们的约束除以消除多项式,仍然是一个多项式,即: ,那么我们就说在 上 成立。
拉格朗日基函数
TODO: explain what a basis is in general (briefly).
多项式通常以单项式基(例如,)来表示。但是当我们在一个 阶乘法子群上工作时,我们 找到了更加自然表示方式,就是以拉格朗日基来表示。
考虑一个 -阶乘法子群 ,它的主单位根是 。则该子群相应的拉格朗日基就是这样一个函数集合 , 其中
我们可以更简洁地写为 其中 就是Kronecker delta函数。
于是,我们可以用拉格朗日基函数的线性组合来表示我们的多项式,
上式其实就等价于我们说 在 的值是 , 的值是 ,在 的值是 , 等等。
当我们在一个乘法子群上工作时,拉格朗日基函数有一个很方便的稀疏表示形式:
其中 质心权重。(欲理解该形式如何推导,请参考3。) 对 ,有
.
假设我们有一系列多项式的值 。 由于我们不能假设 会形成一个乘法子群,我们就用拉格朗日多项式 的一般形式 于是我们构建:
这里,任何 都会产生一个分子为 的项 ,这就导致 整个的积就是 。另一方面,当 时,每一项都是 因此整体的积就是 。于是我们给出了在集合 上的 Kronecker delta 函数 。
拉格朗日插值
设给定一个多项式的点值表示如下,
我们可以利用拉格朗日基重建其系数表示:
其中 。
References
密码群
在章节 群 中,我们引入了 群 的概念。 群有一个单位元和一个群运算。本节,我们将写一个加法群,也就是说,它的单位元是 ,群运算是 。
有些群可以被用于密码学,是为 密码群。这意味着,通常来讲,找到一个在基 下群元素 的离散对数 是困难的。找到离散对数,就是找到一个 使它满足 。
Pedersen承诺
Pedersen承诺 [P99] 是一种以可验证的方式对一个秘密消息进行承诺的方法。 它使用两个公开的、随机的生成元 , 是一个 阶的密码群。 在 上随机选取一个秘密 ,而欲承诺的消息 来自于 的任意一个子集。那么该消息的承诺就是:
为了打开这个承诺,承诺者必须曝露 和 ,以使任何人都能验证 确实是 的承诺。
注意,Pedersen承诺机制是同态的:
假设离散对数假设能够满足,那Pedersen承诺就是完美的隐藏(hiding),计算意义上的绑定(binding)
-
隐藏: 对方选择两个消息 。承诺者承诺其中一条消息 。 给定 ,则对手猜出 的正确值得概率不超过 。
-
绑定: 对方不可能选择两个不同的消息 与随机数 而能使下列等式成立
向量Pedersen承诺
我们可以使用Pedersen承诺的一种变形,来一次性承诺多条消息, 。此时我们需要选取相应数量的随机、公开生成元 ,以及 一个跟以前一样随机的生成元 (用于隐藏)。那么该承诺机制就是:
TODO: is this positionally binding?
Diffie--Hellman
应用密码群的一个例子就是 Diffie--Hellman 密钥协议 [DH1976]。Diffie--Hellman 协议是一种为两个使用者,Alice 和 Bob, 产生一个共享密钥的方法。它的过程如下:
-
Alice 和 Bob 公开协商出两个素数, 和 ,其中 是一个大素数 是 本原根(注意 是群 的生成元)。
-
Alice 选取一个大的随机数 作为她的私钥。她计算她的公钥 ,并把其公钥 发送给 Bob。
-
类似地,Bob 也选择一个大的随机数 作为他的私钥。然后计算他自己的公钥 ,并将其公钥 发送给 Alice。
-
接下来 Alice 和 Bob 都可以计算他们共享密钥 ,Alice 将计算 而 Bob 将计算
潜在的窃密者的目的是在已知 and 这些公开信息下,求解出密钥 。 换句话说,他们不得不从 求解离散对数 ,或者从 中求解离散对数 , 而在 上求解诸如此类的离散对数问题被认为是计算不可能的。
更一般地,密码学中很多协议都运用了与 Diffie--Hellman 相类似的想法。 一个密码群的实例就是 椭圆曲线。在我们进一步探讨椭圆曲线的诸多细节之前,我们将描述一些群上通用算法。
Multiscalar multiplication
TODO: Pippenger's algorithm
Reference: https://jbootle.github.io/Misc/pippenger.pdf
椭圆曲线
在有限域上构造的椭圆曲线是密码学的另一个重要工具。
椭圆曲线就是一个密码群,即:该群上的离散对数问题是困难的。
有许多种定义椭圆方程的方法,就我们而言,我们做如下定义, 是一个巨大的域 (255-bit),有方程 其中 是一个常数, 是它的解,其所有解组成一个集合,我们就称该集合就是在椭圆曲线 上的 -有理点集。 这些坐标 就被称为“仿射坐标”。-有理点集中的所有点与“无穷远点” 就组成了一个群,其中 就是该群的单位元。通常椭圆曲线群用加法来表示。
 "共线三点的和是 , 也就是无穷远点。"
"共线三点的和是 , 也就是无穷远点。"
群加法法则很简单:两个点相加,就是找到过两个点的直线并与椭圆曲线相交于第三个点,并将该点的 坐标取相反数。 自己加自己,也就是二倍点运算,需要进行一些特殊处理:我们求出直线在该点的正切值,进而求出该直线交椭圆曲线的另一点,然后再取逆。 反之,若一个点与它的逆元相加,结果就是无穷远点。
通过点加和二倍点运算,我们很自然就能计算点的标量乘法,即点乘以一个整数,这些整数就被称为 标量。 椭圆曲线点的个数就是群的阶。如果这个阶是个素数 ,于是所有的标量就可以视为 标量域 中的元素。
精心设计的椭圆曲线有一个很重要的安全性质。假定 是 上的两个随机元素,找到一个 使得 , 也就是求解关于 的对应于 的离散对数,在当前经典计算机上,是计算不可能的。这就是椭圆曲线的离散对数假设。
如果椭圆曲线群 的阶是素数 (正如我们在 Halo 2 中所使用的), 则它是一个有限循环群。由上一节 群 可知,这就是说这个椭圆曲线群与 是同构的, 等价地,与scalar域 是同构的。同构由生成元 固定, 进而scalar中的元素就是由 产生的一个群元素的离散对数。在密码学安全的椭圆曲线下,即便同构,也很难在 这种情况下计算,因为椭圆曲线上的离散对数问题是困难的。
有时利用这种同构性质是很有帮助的,方式是在scalars上思考基于群的密码学的协议或者算法,而不是在群元素上。 这会使得证明和表示更加简单。 举例来说,现在在有关证明系统的论文中已经普遍采用 来代表一个有着离散对数 的群元素,显然这种表示中已经隐去了生成元。
我们也如下课题中采用了此一思想, "distinct-x theorem", 用来证明 for elliptic curve scalar multiplication中优化的正确性 以及原始 Halo paper 附录C中所提及的基于同态的优化。
椭圆曲线算术
二倍点运算
求点 的 倍是最简单的情况。继续我们前文的例子,设椭圆曲线是 , 所以第一步计算就是求如下导数:
为了得到计算 的公式,考虑
为了得到 的公式,将 带入椭圆曲线方程:
通过比较 项的系数,我们就得到了 。
射影坐标
上面计算中有求 的逆元的计算,而求逆运算是十分昂贵的。我们可以通过对椭圆曲线方程进行变换来“推迟”求逆运算, 因为通常在一个单独的曲线运算之后,通常并不马上就要得到相关结果的仿射坐标 。基于此一想法,我们引入第三个坐标 并在方程两边同乘以 。如下所示:
特别的,我们最开始的椭圆曲线就是 的情况。令仿射坐标点 可以表示成以下方式 , and ,则我们就得到了一条同态射影曲线
将 转成 是很简单的,只需要在当 时计算 。 (当 时,它就是一个无穷远点 )。在该种表示形式下,计算二倍点时所需要的求逆运算就被推迟了。 一个通常的方法是将 表示成 和 ,转换方程使得分母相同,进一步使结果点 也有一样的分母,使得 。
射影坐标只是在大多数时候,但是并不总是比仿射坐标效率更好。当我们采用不同的方式运用蒙哥马利小技巧, 或者在我们的电路设置中乘法和求逆复杂度形同的情况下(至少是电路规模),就绝非如此。
以下,就给出了基于 的二倍点的计算方法,该方法就是不用求逆的。代入 可得:
进一步得出
注意我们是如何让 和 的分母相同的。综上所述,我们通过令 ,并随之令 和 , 就用射影坐标 的二倍点计算完全替代了直接求仿射坐标 二倍点的计算。通过这种方式, 我们完全避免了在仿射坐标二倍点的计算中所必需的求逆运算,此一方法也会运用到两个不同点的加法中去。
点加
现在计算两个不同点的加法, 加 其中 得到 直线 的斜率是
通过 的表达式,我们可以计算 的 -坐标,即 为:
把直线 的方程带入曲线方程 可得
比较 的系数,可知 .
重要提示:
-
对于无边界情况的点加,存在一个高效的公式1 (所谓的“完全”公式),该公式统一了 点加和二倍点的计算。使用该公式计算一个点和它的逆的加法,将得到 ,也就意味着无穷远点。
-
另外,还有其他的计算模型,比如雅可比表示形式,即:,相比于 ,这是由乘以 的变换得到的。该表示有更好的算术性能,但是却没有一个统一的抑或是完全的公式。
-
在两个同质化的射影坐标空间中,我们可以很方便地比较两个曲线上的点 和 是否相等。方法就是“同一化”他们的 Z-坐标,所以比较两个点是否是同一个点,只需检验如下等式是否成立: 并且 。
椭圆曲线自同态
假设 有三次本原单位根,或者说 ,所以就存在一个元素 ,其能够产生一个 -阶乘法子群。 注意,在示例椭圆曲线 上的点 有两个相关的点:,因为通过计算 都能有效 消除 -坐标的 组成部分。建立映射 就是在曲线上建立了一个自同态映射。这里所涉及到的精确 机制是很复杂的,但是当一条曲线有素数 个点(因而它的阶也是素数),自同态的作用就是对一个点乘以 上的一个标量,相当于在标量域上乘上三次本原单位根 。
椭圆曲线点压缩
给定曲线上一个点 ,它的逆 也在曲线上。 为了唯一表示该点,我们可以仅将其 -坐标和 -坐标的符号进行编码即可。
序列化
正如在 Fields 这一节所提到的,我们可以将一个域元素的最低位作为其“符号”。 因为它的加法逆元总是有相反的最低位。所以我们就把 -坐标的最低为作为其“符号”。
Pallas 和 Vesta 是定义在域 和域 上的,二者的元素都是 bits。
它的表示需要32个字节,同时还会剩余一个bit。于是,我们就将 -坐标的 符号位 放入 -坐标的最高位即可:
<----------------------------------- x --------------------------------->
Enc(P) = [_ _ _ _ _ _ _ _] [_ _ _ _ _ _ _ _] ... [_ _ _ _ _ _ _ _] [_ _ _ _ _ _ _ sign]
^ <-------------------------------------> ^
LSB 30 bytes MSB
“无穷远点” 作为群的单位元并没有相应的仿射坐标 表示。但是,可以证明,不论是 Pallas 还是 Vesta 曲线都没有 或 的点。因此,我们就可以使用“假的”仿射坐标 来代表 ,那么它的实际表示也就是一个全为 的32字节的数组。
反序列化
一个压缩的椭圆曲线的点的放序列化方法是,首先读取最高位作为 y符号,这个符号就是 -坐标的符号。
第二步,将该位设为0以得到真正的 -坐标。
如果 我们就返回一个“无穷远点” 。反之,我们就进一步计算 。
接下来,我们可以读取计算出来的 -坐标的最低位,也就是它的 符号,如果
sign == ysign, 我们就得到了正确的结果,只需将 返回即可。反之,我们就对 取反并返回 。
曲线循环
令 是定义在有限域 上的椭圆曲线,其中 是素数,记为 , 并且我们记定义在 上的群 的阶是。对这条曲线,我们称 为“基域”, 为“标量域”。
我们在 实例化我们的证明系统。这允许我们证明关于 算术电路的满足性命题。
(备注) 既然椭圆曲线 是定义在 上,那为什么算术电路却实现在 上? 证明系统基本上就是工作在由标量组成的电路上 (或者,更准确地,标量其实是要承诺的多项式的系数)。 标量就在 上,当它们编码或者承诺的对象是椭圆曲线 上的点。
与之相应,绝大多数验证者的算术运算都是在基域 上的,因此可以用 的算术电路高效的表示。
**(备注)为什么验证计算 (主要) 发生在 上? ** 事实上,Halo 2 对电路的输出做一些群运算。而群运算,就如二倍点和点加就会用到域 上的算术运算, 因为点的坐标都在域 上。
这促使我们构造以 为标量域的另外一条曲线,这条曲线实现一个基于 的算术电路,该电路就可以有效地 来验证来自第一条曲线的证明。更美好的是,如果这条曲线的基域又是 ,那么它生成的证明就又可以被第一条曲线的 算术电路所验证。于是就形成了一个2-曲线循环:

TODO: Pallas-Vesta curves
Reference: https://github.com/zcash/pasta
Hashing到椭圆曲线(??)
有时将某个输入映射到椭圆曲线 上的随机一个点是很有用的,这样,就没人能知道它的离散对数(相对其他基)。
相关细节在 Internet draft on Hashing to Elliptic Curves 中有所描述。 针对效率和安全性,有各种各样的算法完成这个工作。Internet Draft 所使用的框架就运用了多种功能:
-
hash_to_field: 将一个字节序列映射到基域 上的一个元素 -
map_to_curve: 将 上的元素映射到 上。
TODO: Simplified SWU
Reference: https://eprint.iacr.org/2019/403.pdf
References
使用内积证明的多项式承诺
我们欲对 进行承诺,并且可以在任意一点验证承诺的多项式的正确性。 最简单的解决方案就是证明者将多项式的系数发给验证者。但是这种方法需要 次通信。我们的 多项式承诺机制可以仅用 次通信就完成工作。
Setup
给定一个参数 ,并且生成了CRS(common reference string), 并定义了该机制中的一些常数:
- 是一个 阶的群,其中 为一个素数;
- 是 维向量,它的元素都是在群元素中随机挑选;
- 是一个随机的群元素;
- 一个 -阶有限域。
Commit
定义Pedersen向量承诺为
其中 是欲承诺的多项式, 是盲化因子。 向量 中的每一个元素 就是多项式 ,的第 项的系数。而 的最大次数是 。
Open (prover) and OpenVerify (verifier)
经过修改的内积证明是对如下关系信息的一种证明:
其中 而 是欲求值的点。 内积证明就使证明者能够向验证者证明,承诺 中所承诺的多项式,在 处的值就是 ,还有 承诺的多项式的最大阶数是 。
内积证明将进行 轮。就我们的目的来说,我们只要知道最终输出就足够了,所以我们只是对 中间轮提供一个直观的描述。(请参考 Halo 论文,以获取全面的解释)。
在开始证明之前,验证者要随机选取一个群元素 并将它发送给证明者。 我们在第 轮将对所需向量做如下初始化, , 。在每一轮 :
- 证明者都要用 , 和 进行内积计算得到两个值 和 。 这里要“交叉项”("cross-terms")有个概念,即: 的低半部分与 和 的高半部分运算,反之亦然。
-
验证者发送一个随机挑战 ;
-
证明者就使用 将 的低半部分与高半部分压缩乘只有原向量一半的新的向量。 向量 和 也进行类似的压缩,从而得到 和 .
-
, and 是下一轮,即 轮的输入。
注意在最后一轮,即 轮,我们只剩下 , , 每个向量的长度都是1。直观讲, 这些最终的标量,和每一轮的 以及每一轮的“交叉项” , 实际上是编码了每一轮的压缩操作。由于证明者并不能事先知道挑战 ,他们就不能人为操控每一轮的压缩。因此,验证最后这些项的约束就能证明每一轮的压缩都是正确的, 同时也证明了在压缩开始前原始 就满足特定的关系。
事实上,每一轮的 就是公开信息 与 计算出来的, 因此验证者可以自己计算每一轮的 ,以验证证明者是否提供了正确的值(二者值应该相等)。
递归
Alternative terms: Induction; Accumulation scheme; Proof-carrying data
计算 需要计算长度 多倍点 其中 每一轮挑战 按照二进制查数的顺序进行排列组成的。 在多个证明的验证中,我们希望平摊这个线性计算。 和计算 不同, 我们可以将 表示成一个多项式的承诺
其中 是一个 次多项式。
 | 由于 是一个承诺,它就可以在内积证明中被验证。验证电路的 witnesses 并产生 做为证明 的公开输入。下一个验证者将运用内积证明来检查 ;这包括对给定的挑战 ,查验 在某个随机点处的值是不是正确。依据 上一章节 我们知道,该检查仅需要 的工作。 在检查 和 的最后阶段,验证电路将产生 ,和 挑战。为了彻底证明 合法的,我们需要计算 ,这是一个线性时间复杂度的计算。接下来,我们通过将 作为电路的witness和公开 做为证明 的公开输入推迟了这个计算。 由此,我们可以不断地从一个证明到另外一个证明,直到满足了我们需要的证明的个数,该过程才会中止。我们只需在最后做一次线性时间复杂度的计算,就可以证明之前产生的所有证明都是合法的。 |
依据上文所述 曲线的循环,我们可以用2-cycle的曲线来实现一个协议,这就是说,在一条曲线上产生证明, 而在另一条曲线的电路中进行验证。但是又有某些验证计算在原有的曲线上(证明产生的曲线)效率更高;这些就被“推迟”到下一个本地电路(请看下图) 而不需要立即送到另外一条曲线上。