执行轨迹（Execution trace 或者 trace）

执行轨迹是由执行某个计算时，一组机器状态序列构成。说得直白点，就是为了执行某个程序C，申请了W个寄存器，执行了N个步骤，那么执行轨迹可以用一张大小为$N\times W$表来描述。

以斐波那契数列计算为例，可参考ZKHack Mini2 Can you turn up the heat?

fn fib(start: (Felt, Felt), n: usize) -> Felt {
    let mut t0 = start.0;
    let mut t1 = start.1;

    for _ in 0..(n - 1) {
        t1 = t0 + t1;
        core::mem::swap(&mut t0, &mut t1);
    }
    t1
}

可以看到这里使用了2个寄存器，s0、s1分别存放每一个中间状态下的数据。模拟n = 10的时候，生成的执行轨迹是一个数组，包含了5对中间状态数据(state[0],state[1])。这里的执行轨迹是由prover定义并生成的，源码如下：

	pub fn build_trace(start: (Felt, Felt), n: usize) -> TraceTable<Felt> {
        
        let mut trace = TraceTable::new(2, n / 2);
        trace.fill(
            |state| {
                state[0] = start.0;
                state[1] = start.1;
            },
            |_, state| {
                state[0] += state[1];
                state[1] += state[0];
            },
        );

        trace
    }

执行轨迹中的数据如下图所示。

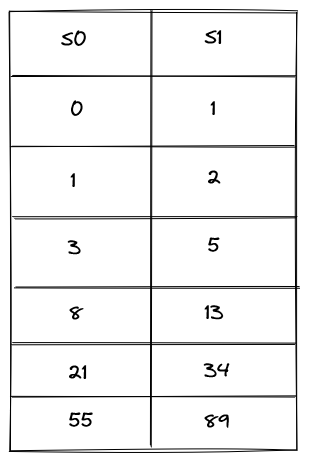
这样定义出来的执行轨迹只有2列，状态转换的具体约束条件如下：

		result[0] = next_state[0] - (current_state[0] + current_state[1]);
    result[1] = next_state[1] - (current_state[1] + next_state[0]);

也就是说，每一次状态转换必须满足这2个约束：

1. s_{0, i+1} = s_{0, i} + s_{1, i}
2. s_{1, i+1} = s_{1, i} + s_{0, i+1}

相应的约束多项式的度最大为1。因此，创建AIR时，定义状态转换的约束多项式的度为1。

		let degrees = vec![
            TransitionConstraintDegree::new(1),
            TransitionConstraintDegree::new(1),
        ];

此外，AIR中还需要对输入、输出进行约束，参考如下：

		vec![
            Assertion::single(0, 0, self.start.0),       // input contraint
            Assertion::single(1, 0, self.start.1),       // input contraint
            Assertion::single(0, last_step, self.end),   // output contraint
        ]

至此，我们就构建了执行轨迹，并根据执行轨迹构建了对应的约束。

实际上，构建一个合理执行轨迹，并据此设计无懈可击的约束系统是学习并使用ZK-Stark非常重要的一步。如果感兴趣，可以参考**ZKHack Mini1: There’s something in the AIR ** ，帮助更深入地理解AIR。