ZK-STARK 证明系统

STARK 中的多项式承诺

两种类型的多项式

从算术化的约束系统中，我们会得到两种类型的witness，第一是整个待证明程序的执行轨迹，也叫做execution trace，第二是在执行过程中需要满足的约束条件，称为 constraint。

执行轨迹可以看成是一组寄存器的状态转换过程。这里我们仍以斐波那契数列的计算为例，假设我们要求出 fib(10)，且用两个寄存器 s0, s1 来保存计算的中间状态，那么在程序正确执行5步后，s0[5] 就是我们需要的计算结果。

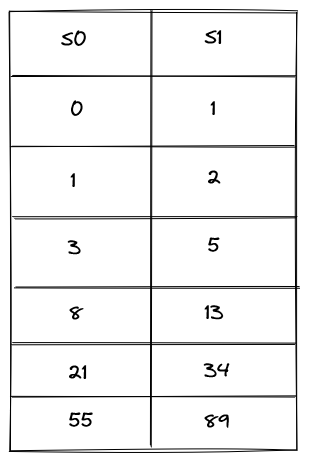
有了程序的执行轨迹，我们还需要额外的约束来保证执行轨迹确实是程序按照我们给出的计算方式来生成的。约束分为两部分：

1. 在边界处，寄存器的状态必须和指定的寄存器状态一致。例如 s0, s1 的初始状态要满足 s0[0] = 0 且 s1[0] = 1。另外，我们得到的计算结果必须是程序执行到第5步后 s0 寄存器的状态，即 result = s0[5]。
2. 寄存器每一次的状态转换必须满足如下计算规则：
   1. s0[i] + s1[i] = s0[i+1]
   2. s1[i] + s0[i+1] = s1[i+1]

有了这些约束，我们就能够信任程序的执行结果，即 fib(10) = result = s0[5] 了。接下来我们需要对执行轨迹和约束条件做多项式承诺。

承诺一个多项式

在讲具体的实现之前，我们先来了解 STARK 中是如何对一个多项式进行承诺的。我们知道一个多项式承诺方案（polynomial commitment scheme）需要满足如下使用场景：

1. 设置：能够生成特定的代数结构 $\mathbb{G}$，以及公私钥对 $⟨PK,SK⟩$ ，用于承诺一个度数小于 $t$ 的多项式
2. 承诺：输出多项式 $\varphi (x)$ 的承诺 $\text{C}$
3. 打开：对于验证者给定的 $i$，证明者给出多项式在该点处的值 $\varphi (i)$，以及关于该求值的一个证明。验证者能够利用之前的承诺 $\text{C}$ 验证其求值是正确的

在常见的 $KZG$ 多项式承诺方案中，证明者首先使用椭圆曲线点乘的方式，对多项式进行承诺，随后在打开时构造一个新的商多项式，使得验证者可以通过椭圆曲线配对，验证该商多项式正是原始的 $\varphi (x)$ 在挑战点处构造出的多项式。具体的步骤可以参考 $KZG$ 的论文，这里不再赘述。

STARK 使用默克尔树进行多项式承诺，实现方式如下：

1. 设置：STARK不需要额外的可信设置，但需要事先确定用于构造默克尔树的哈希函数
2. 承诺：首先求出多项式 $\varphi (x)$ 在其求值域上所有单位根处的值，$\varphi ({\omega }^0),\varphi ({\omega }^1),\varphi ({\omega }^i),...$，以这些值为叶子节点，组成一颗默克尔树，最后公开得到的默克尔树树根，即是该多项式的承诺。
3. 打开：验证者选定随机挑战点，证明者提供多项式在该点处的值，以及一条默克尔树路径。验证者检查该默克尔树路径合法。

轨迹多项式（Trace Polynomial）的承诺

对于任何一个 STARK 寄存器的执行轨迹，我们可以将它的每一行看作是其对应的轨迹多项式在某个单位根处的取值。因此，对于示例中的 $s0(x),s1(x)$，我们有：

$$\begin{gathered} s0({\omega }^0)=0,s1({\omega }^0)=1 \\ s0({\omega }^1)=1,s1({\omega }^1)=2 \\ s0({\omega }^2)=3,s1({\omega }^2)=5 \\ s0({\omega }^3)=8,s1({\omega }^3)=13 \\ s0({\omega }^4)=21,s1({\omega }^4)=34 \\ s0({\omega }^5)=55,s1({\omega }^5)=89 \end{gathered}$$

因为默克尔树要求叶子节点个数必须是2的幂次，这里我们需要补上程序继续按约束条件运行的结果：

$$\begin{gathered} s0({\omega }^6)=144,s1({\omega }^6)=233 \\ s0({\omega }^7)=377,s1({\omega }^7)=610 \end{gathered}$$

这样就可以为 $s0(x),s1(x)$ 分别生成默克尔树承诺了。不过请稍等，为了协议的安全性，我们还需要进行扩展。

低度多项式扩展（Low-Degree Extension）

从程序的执行轨迹中，我们得到了数个长度为 $N$ 的轨迹多项式。实际的使用场景里，出于安全性的考虑，我们需要在一个更大的求值域上承诺该多项式，一般需要将求值域扩大 $2^k$ 倍，扩大的倍数称为爆炸倍数（ blowup factor），该求值域称为 $LDE$ 域。

我们会在 DEEP-FRI 章节讨论安全性的问题。现在来看如何将长度为 $N$ 的轨迹多项式扩展到 $2^{k}N$ 。我们先利用拉格朗日插值法，求出该轨迹多项式的各项系数 $a_0,a_1,a_2,..,a_{n-1}$ （注意其单位根需要使用 $2^{k}N$ 求值域上的单位根），然后我们在 $2^{k}N$ 的求值域上用系数求出其他单位根处的多项式值。这种利用一个低次多项式生成更大的求值域上单位根处值的方法称为低度多项式扩展。

下图是 blowup factor = 2 时， $s0(x)$ 的低度多项式扩展示例，黄色的节点是多项式在原始的求值域上对应单位根处的值（它们也是在 $LDE$ 域上所有单位根处值的一部分，因为 ${\omega }_{origin}^i={\omega }_{LDE}^{2^k\ast i}$ ），蓝色为 $LDE$ 扩展后新的单位根处的求值：

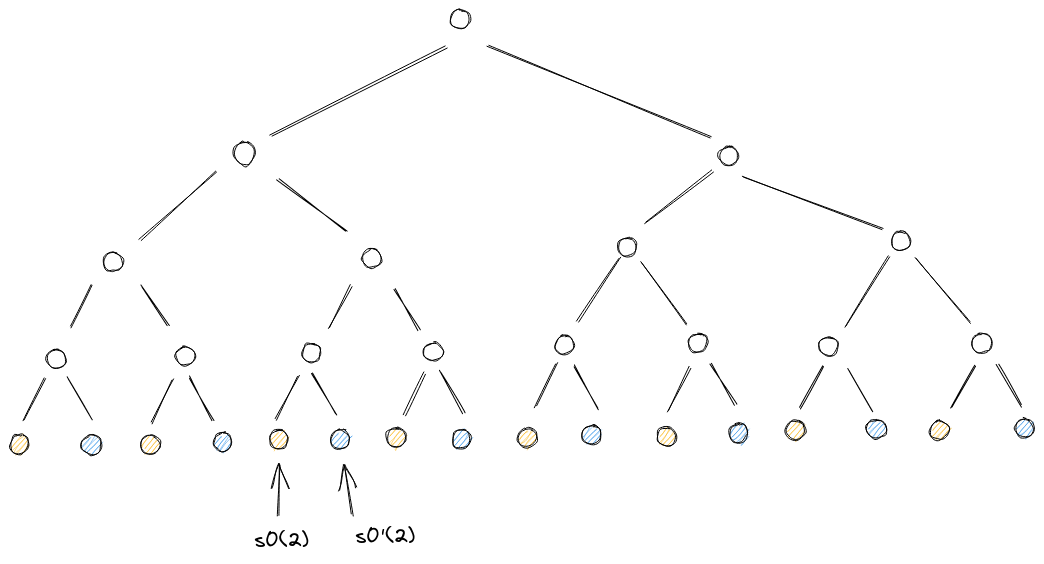
约束多项式（Constraint Polynomial）的承诺

程序在执行过程中需要满足的约束条件，同样也可以转换为多项式来表示。例如，我们要约束 $s0({\omega }^5)=55$，可以按如下的方式构造约束多项式：

$c(x)=\frac{s0(x)-55}{x-{\omega }^5}$

根据多项式基本定理，$s0(x)-55$ 可以被 $x-{\omega }^5$ 整除当且仅当 $s0({\omega }^5)=55$。也就是说，当约束条件满足的时候， $c(x)$ 的次数小于 $s0(x)$。我们利用这种方法，将所有的约束条件写成多项式的形式：

1. $c0(x)=\frac{s0(x)-0}{x-{\omega }^0}$
2. $c1(x)=\frac{s1(x)-1}{x-{\omega }^0}$
3. $c2(x)=\frac{s0(x)-55}{x-{\omega }^5}$
4. $c3(x)=\frac{s0(\omega x)-s0(x)-s1(x)}{{\prod }_{i\in [0,6]}x-{\omega }^i}$
5. $c4(x)=\frac{s1(\omega x)-s0(\omega x)-s1(x)}{{\prod }_{i\in [0,6]}x-{\omega }^i}$

将约束多项式组合起来

如果一个个检查约束多项式的次数，代价会很大，也没有必要。我们可以将所有的约束多项式组合到一起，形成一个组合多项式（Composition Polynomial），对该组合多项式的检查即是对所有约束多项式的检查。

在组合之前，有一点要注意：上述的约束多项式的次数不是相同的。需要先将约束多项式补齐到相同的次数，然后再组合。补齐的方法是将它乘上一个随机的 $D-D_j$ 次多项式，该随机多项式的系数是验证者在证明者承诺完轨迹多项式后随机产生的。

$CP(x)={\sum }_{j=0}^4{c}_j(x)(\alpha x^{D-D_j}-{\beta }_j)$

最后我们得到 组合多项式 $CP(x)$，别忘了我们需要在 $LDE$ 域上承诺它，因此也要像之前的轨迹多项式那样，使用低度多项式扩展的方式进行承诺。

DEEP-FRI

得到轨迹多项式和组合多项式后，其实我们已经可以进行证明了。只要把轨迹多项式和组合多项式再做一次随机的线性组合，然后证明最终的多项式度数小于 $D$ ，就能证明所有的约束条件满足，且程序的执行过程和被承诺的Trace一致。

但是，从安全性角度出发，还需要做一些调整。STARK 使用称为 Domain Extension for Eliminating Pretenders (DEEP) 的方法进行检查。我们需要从基域上随机选一个点，然后检查在这个点上，各多项式的值是否满足约束。基域是自变量 $x$ 的取值范围 $\mathbb{F}$ ，是一个比 $LDE$ 域大得多的域。

设我们挑选了随机点 $z\in \mathbb{F}$ ，则 $DEEP$ 多项式可以构造为：

$DEEP(x)={\alpha }_0\frac{s0(x)-s0(z)}{x-z}+{\alpha }_1\frac{s1(x)-s1(z)}{x-z}+{\alpha }_2\frac{CP(x)-CP(z)}{x-z}$

在实际应用中，$CP(x)$ 的度数一般比轨迹多项式要高，取决于约束条件。如果约束条件有两列相乘（即二次的约束），则 $CP(x)$ 的度数就为 $2D$ 。这种情况下，需要将 $CP(x)$ 拆分为多个次数小于 $D$ 的多项式。本文中因为约束是一次的，因此 $CP(x)$ 的次数和轨迹多项式的次数一致。另外，上面构造的 $DEEP(x)$ 多项式，正常来说其次数应该小于 $D-2$ （因为分子均为次数小于 $D-1$ 次的多项式，而分母为 $1$ 次多项式）。但为了后面做 FRI 承诺的时候计算方便，我们仍然通过乘上一个多项式的方式，将其次数升高一次，这样它的次数应该小于 $D-1$ 。

关于构造 $DEEP(x)$ 多项式的必要性，可以参考 Eli Ben Sasson 的文章 DEEP-FRI: Sampling Outside the Box Improves Soundness

构造完 $DEEP(x)$ 后，如果能够证明 $DEEP(x)$ 是一个次数小于 $D-1$ 的多项式，就可以证明所有的多项式在 $z$ 点处的取值即是所预期的值，进而证明程序的执行结果正确，且所有的约束条件都满足。

FRI 低度多项式测试

低度多项式测试的原理

怎样证明一个多项式 $f(x)$ 的次数小于特定的 $D$ 次呢？低度多项式测试提供了一种方法，即：从 $f(x)$ 上任意挑选 $D+1$ 个点值对 $(x_i,f(x_i))$，使用其中的 $D$ 个点值对构造一个 $D-1$ 次多项式 $f^{\prime }(x)$ 。若 $f^{\prime }(x)$ 和 $f(x)$ 在第 $D+1$ 个点处的求值相等，则有较大的概率 $f(x)$ 是一个次数小于 $D$ 的多项式。

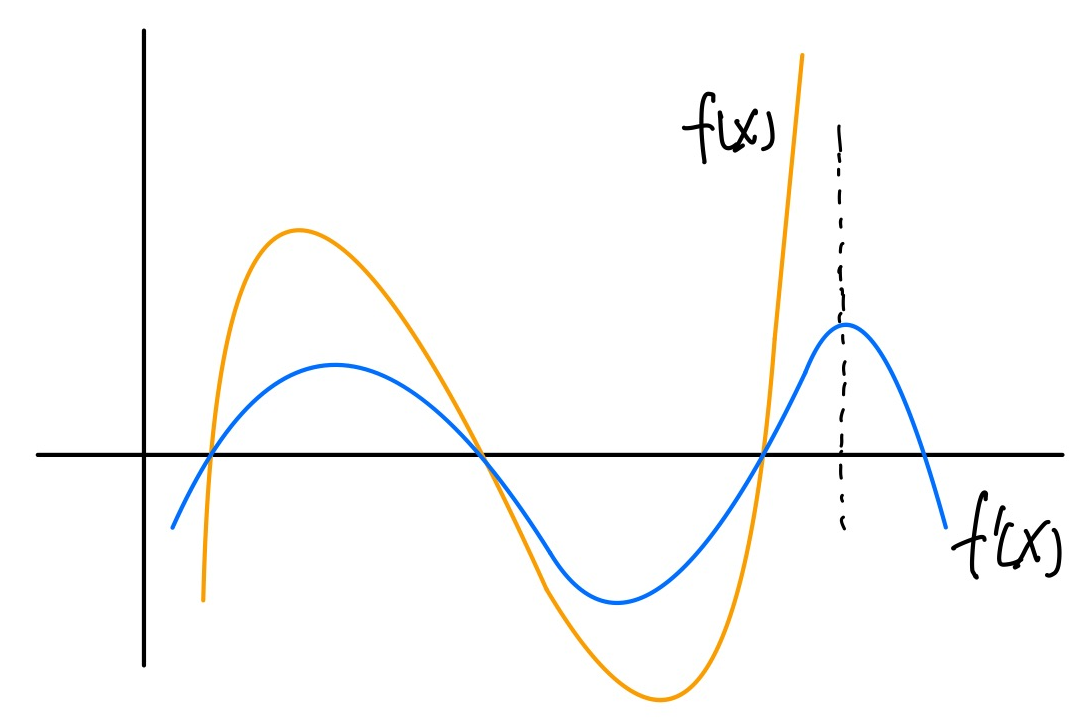
出于安全性的考虑，可以将这个过程重复 $k$ 次。若进行一次测试，证明者作弊成功的概率为 $p$，那么挑选 $D+k$ 个点值对，证明者成功的概率就是 $p^k$ 。

使用折叠减小开销

上述低度多项式测试的方法有一个缺点，即构造 $f^{\prime }(x)$ 需要 $D+k,k\ge 1$ 个点值对，在多项式度数非常大的前提下，测试需要的时间和通信量也会变得无法承受。FRI 通过一种称为“折叠”的方法，降低了通信开销。具体做法是：

1. 首先将所有的 $n$ 个点值对 $(x_i,f(x_i))$ 按 $N$ 列进行划分，得到一个 $\frac{n}{N}$ 行，$N$ 列的矩阵
2. 证明者需要承诺矩阵的每一行，承诺的方式是将一行中所有的 $f(x_i)$ 进行哈希，得到共$\frac{n}{N}$ 个哈希值，组成默克尔树并输出树根
3. 对应每一行，证明者将该行的所有点值对使用随机数 $\alpha$ 进行线性组合： $f^{\prime }(x_i^{\prime })=f(x_i)+\alpha f(x_{i+1})+...+{\alpha }^{j}f(x_{i+j})+...+{\alpha }^{N-1}f(x_{N-1})$
4. 注意到，如果我们精心挑选 $x_i$，则得到的新多项式可以看成原多项式的每一项按模 $N$ 划分出的多项式的组合，其系数正是原多项式对应项系数的线性组合
5. 这样我们得到了一个项数为 $\frac{n}{N}$ 的多项式 $f^{\prime }(x)$ ，再次重复1-4步，直到我们将新多项式的次数降到可以承受的范围之内。
6. 假设我们重复了 $k$ 次，则只需检查最后的多项式次数是否小于 $\frac{D}{N^k}$ 即可

第4步的解释：

我们构造的新 $f^{\prime }(x_i)$ 可以看成是 $N$ 个多项式的线性组合，假设原来的多项式的求值域上单位根分别为 ${\omega }^0,{\omega }^1,{\omega }^2,...,{\omega }^n$ ，那么新的多项式其求值域是原来的 $1/N$ ，其单位根变为 ${\omega }^0,{\omega }^N,{\omega }^{2N},...,{\omega }^{\frac{n}{N}\ast N}$

$f^{\prime }({\omega }^0)=f({\omega }^0)+\alpha f(w^0\ast w^1)+{\alpha }^{2}f({\omega }^0\ast {\omega }^2)+...$

$f^{\prime }({\omega }^N)=f({\omega }^N)+\alpha f(w^N\ast w^1)+{\alpha }^{2}f({\omega }^N\ast {\omega }^2)+...$

$f^{\prime }({\omega }^{2N})=f({\omega }^{2N})+\alpha f(w^{2N}\ast w^1)+{\alpha }^{2}f({\omega }^{2N}\ast {\omega }^2)+...$

令 $u(x)=f(x\ast \omega ),v(x)=f(x\ast {\omega }^2),w(x)=f(x\ast {\omega }^3),...$ ，则有

$f^{\prime }(x)=f(x)+\alpha u(x)+{\alpha }^{2}v(x)+...,x\in [{\omega }^0,{\omega }^N,...]$

可见 $f^{\prime }(x)$ 是次数为 $\frac{n}{N}$ 的多项式

验证者的检查

检查FRI步骤的正确性

首先，因为证明者每次 FRI 折叠的时候都承诺了折叠后所有新点值对的默克尔树，验证者只需在同一层上抽取 $N$ 个相关的折叠点，在下一层上抽取一个点，就能验证本层的 $N$ 个点确实按正确的随机数折叠到了下一层的同一个点。

其次，验证者检查最后余下的多项式是否满足度数小于 $\frac{D}{N^k}$ ，这个使用低度多项式测试进行抽查即可验证。

检验多项式是否匹配

事实上，证明者如果伪造一个 $DEE{P}_{fake}(x)$ ，它的度数小于 $D$ ，那么它总是能够通过低度测试。 因此验证者需检查：通过 FRI 低度测试的多项式，确实为证明者构造的 $DEEP(x)$ 多项式。验证者可以向证明者请求 $LDE$ 域中任意一点处的 $DEE{P}_{fake}(x)$ 的值，以及之前的轨迹多项式，组合多项式在该点处的值 $s0(x),s1(x),CP(x)$ 。验证者自行计算 $DEE{P}_{real}(x)$ ，若它和证明者发送的 $DEE{P}_{fake}(x)$ 不匹配，则验证不通过。

如果证明者想要伪造 $DEE{P}_{fake}(x)$ ，他需要让该多项式的度数小于 $D$ 。因此若原始的 $DEE{P}_{real}(x)$ 是个高次多项式（次数很高，远高于 $LDE$ 求值域的度数），则二者在 $LDE$ 上最多可以在 $D$ 个求值点处相等（若有多于 $D$ 个求值点相等，则伪造的多项式 $DEE{P}_{fake}(x)$ 次数必定大于等于 $D$ ）。此时，验证者随机检查一个求值点，两个多项式在点处值相等的概率即为 $1/2^k$ （ $k$ 为爆炸倍数）。验证者可以多次重复这一过程，直到证明者作弊成功的概率小于目标安全参数即可。

ZKHack-Mini 上有一个证明者通过伪造 $DEEP(x)$ 进行攻击的例子，可以参考 ZKHack-Mini: Puzzle 2 。

磨损因子(Grinding Factor)

因为上述的验证手段均为概率的，为防止证明者靠庞大的计算能力进行反复重试，可以要求证明者在提供 STARK 证明的同时也提交一个工作量证明 （PoW），使得重试的代价变大。

参考文献

StarkDEX Deep Dive: the STARK Core Engine

ethStark

Vitalik STARK series I: Proofs with Polynomials

Vitalik STARK series II: Thank Goodness It's FRI-day

Vitalik STARK series III: Into the weeds

DEEP-FRI: Sampling Outside the Box Improves Soundness

ZKHack