StarkDEX Deep Dive: the STARK Core Engine

引言

(译者按：本文翻译自Medium中的同名文章)

这是深入了解StarkDex系列的第三部份。我们在这个系列介绍一个通用的STARK证明系统，当中包括StartDex。如果你还没有对StarkDEX的整体了解，建议先阅读第一部份及第二部份，你亦可独立阅读本文。我们亦建议你阅读 Stark数学系列，当中深入讨论本文中的数学架构。

本文中，我们形容STARK证明系统为一个证明者(prover)和验证者(verifier)之间的交互式协议。证明者发出一系列的讯息试图说服验证者一个特定的计算己被正确地执行(已验证陈述)。验证者则以随机数回应该讯息。最后，如果计算真的被正确执行，验证者会接受该证明；否则，验证者(有很高概率)拒绝接受。

注意，这里我们形容Stark系统为一个交互式协议，在Alpha版本的StarkDEX，非交互式系统最终会取代交互式系统。在非交互式系统，证明者提供一个证明后，验证者直接决定是否接受。

STARK证明系统

想重温执行追踪(execution traces)及多项式约束(polynomial constraints)，可阅读Stark数学系列中算术化(Arithmetization)一及二。

轨迹

一个计算的执行轨迹，或简称轨迹，是一个机器状态的序列 — 每个时钟周期一个。如果一个计算需要 w 个寄存器和 N 个周期，执行轨迹可表达为一个 N x w 的表。要证明一个有关计算正确性的陈述，证明者首先要计算出一个轨迹。

将轨迹的列表达为f₁, f₂,…, fs 。每一个 fⱼ 的长度都是N=2ⁿ ，n是一个固定的值。 轨迹单元内的值是一个大域F的元素。在Alpha 版本，Ｆ是一个252 位的质数域。轨迹求值域定义为 ，其中 g 是 F 的乘法群的子群中的生成元。 实际上，我们以 的元素去代表轨迹的行。 每个轨迹列被视为在轨迹求值域上对次数小于 N 的多项式的 N 次逐点求值。这些多项式可被称为轨迹列多项式(trace column polynomials)，或简称列多项式(column polynomials)。

轨迹低度扩展 (Trace Low Degree Extension) 及承诺 (Commitment)

如前所述，每个轨迹行可视为一个度数低于Ｎ的Ｎ求值。要达至一个安全的协议，每个这样的多项式都要在一个更大的域求值，该域称为求值域(evaluation domain)。例如，在StarkDex Alpha，求值域的大小通常是16*N。我们称这个求值为轨迹低度扩展(Low Degree Extension, LDE)，而求值域与轨迹域之间的比例称为爆炸倍数 (熟悉编码理论的人会发现爆炸倍数是 1/rate，而LDE实际上是轨迹的里德-所罗门编码(Reed-Solomon code))。

证明者在产生轨迹LDE后，将其承诺。整个系统，承诺通过建立一系列域元素的默克尔树(Merkle tree)来实现，默克尔树的根会发送到验证者。后者涉及几个工程学上的考虑，包括域元素序列化及哈希函数的选择－为令文章更简洁，详情在此略过。

有关默克尔树叶子的选择，如果一个承诺打开可能牵涉多个域元素，它们最好集中在同一个默克尔树叶子。在轨迹LDE的情况，这意味着所有轨迹LDE“列”(所有在gⁱ点的行多项式的求值) 的域元素会被集中在同一个默克尔树叶子。

约束

一个执行轨迹只在符合以下条件才成立：(1)某些边界约束成立，及(2)每对连续状态都满足计算规定的约束。例如，在某一时间点 t，第一个和第二个寄存器的内容相加，把结果放在第三个寄存器，相关的约束是： $Trace[t,1]+Trace[t,2]-Trace[t+1,3]=0$　。

当且仅当计算正确时，约束表示为轨迹单元上组成的多项式。因此，它们被称为轨迹的代数中间表示多项式约束 (Algebraic Intermediate Representation, (AIR) Polynomial Constraints)。例如，证明去中心化交易所(Decentralized Exchange, DEX)执行的一批交易的正确性时，约束成立当且仅当这批交易都有效。

以下看看几个不同的约束例子：

1. f₂(x)-a = 0 for x=g⁷ (第二列第 g⁷ 行的值等于 a)
2. f₆²(x) -f₆(g³x) = 0 for all x (每行第六列的值的平方等于三行前的值)
3. f₃(x) -f₄(gx) = 0 for all x but g⁵ (每行第三列的值等于前一行第四列的值，除了第g⁵行外)
4. f₂(x) -2*f₅(x) = 0 for all x in an odd row (奇数行第二列的值等于该行第五列的值的双倍)

我们的目标是证明一个计算是否正确。写出一套当且仅当计算有效才成立的多项式约束，我们把原本的问题简化成证明多项式约束成立。

由多项式约束至低度测试问题

接下来，我们将每项约束表达成一个有理函数。上面的约束(1)翻译成

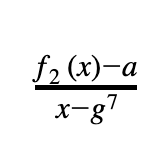
这个多项式的度数最高为 deg(f₂)-1 当且仅当约束(1)成立 (详情参看 Arithmetization 1）。要明白约束(2), (3)和(4)，首先回忆一下以下集合{x∈ F | xᴺ-1=0} 正好等于乘法群F 中的所有 x 。所以，我们得出以下的简化结果：

• 约束(2)成立当且仅当以下有理函数是一个度数最多为2*deg(f₆)-N的多项式：

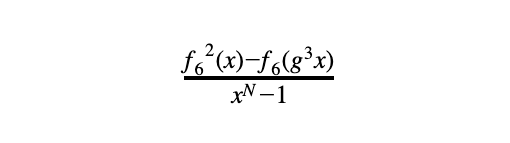
• 约束(3)成立当且仅当以下有理函数是一个度数最多为max{deg(f₃), deg(f₄)} — N+1的多项式：

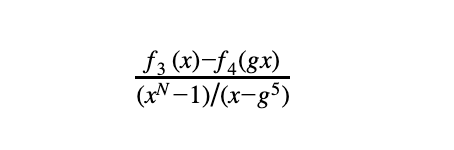
• 约束(4)成立当且仅当以下有理函数是一个度数最多为max{deg(f₂), deg(f₅)} — N/2的多项式：

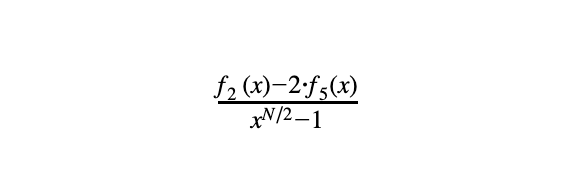
当约束表达成有理函数时，分子定义了需要在轨迹执行的规则；分母则定义相关规则应该成立的域。由于验证者需要求这些有理函数的值，STARK系统的简洁非常重要，分母定义的域需要被快速地求值，如上述四个例子。

组合多项式

为了高效地证明执行轨迹的有效性，我们力图达到以下三个目标：

1. 在轨迹多项式之上构建约束。
2. 调整不同度数的约束至同一度数，以令它们可以合拼成一个该度数的多项式。
3. 合拼所有约束至一个(更大的)多项式，称为组合多项式，使得只要一个低度数测试即可证明所有约束的(低)度数。

本节讨论以上如何实现。

度数调整

要确保可靠性，我们要显示所有以轨迹列多项式建构的所有约束都是低度数。因此，我们把约束的整体度数调整为所有约束之中最高的一个，称为D (如果D不是2的幂，则向上调整至最接近的2的幂)。D即为组合多项式的度数。

度数调整方法如下：

给定一个度数 Dⱼ 的常数 Cⱼ(x)，我们以以下形式加进组合多项式

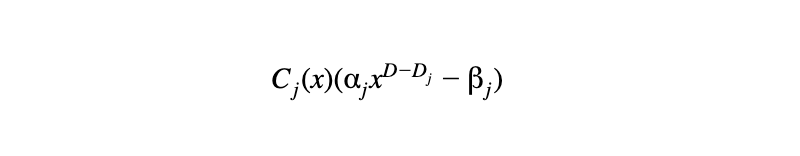
当中𝛼ⱼ 及 βⱼ 是验证者发来的随机域元素。结果，如果组合多项式是低度数，每个独立约束便会自动是低度数。结果是一个以下形式的组合多项式。

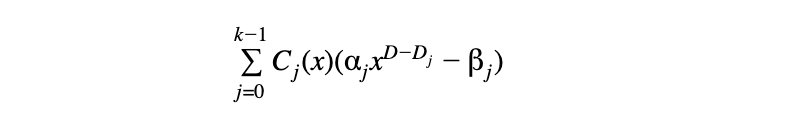
当中k是常数。

约束组合

一旦证明者已承诺轨迹 LDE，验证者将提供随机系数以创建约束的随机线性组合，从而产生合成多项式。无需单独检查每个约束在轨迹元素上的一致性，只需对组合多项式应用低度测试即可，该组合多项式表示一次应用于所有轨迹的所有约束。

由于我们的 Alpha 版本中使用的约束为 2 度或以下，因此组合多项式的度数为 2N。我们可以将组合多项式 H(x) 表示为长度为 2N 的单列求值，或者，我们更倾向将其表示为长度为 N 的两列 H₁(x) 和 H₂(x)，其中 H(x) =H₁(x²)+xH₂(x²)。

承诺组合多项式

接下来，证明者对H 1 和 H 2 的两个组合多项式列再次进行低度扩展。由于这些列与轨迹列的长度 N 相同，我们有时将它们称为组合多项式轨迹，并且我们以与执行轨迹多项式相同的方式进行扩展和承诺。这是通过将它们扩展相同的爆炸倍数来完成的，将同一行的域元素作为默克尔树的叶子，计算哈希值并将树的根作为承诺发送。

随机点的一致性检查（DEEP 方法）

注意，给定点（域元素）z 的 H(x) 值可以通过两种方式获得：从 H1(z²) 和 H2(z²) 或通过计算上述的约束线性组合。该计算在需要计算的轨迹列上产生一组点，以完成所需的计算。计算单个点的 H(x) 所需的点集称为掩码(mask)。因此，给定一个点 x=z，如果给定 H₁(z²) 和 H₂(z²) 的值以及轨迹上的对应的掩码值，我们可以检查 H 和轨迹之间的一致性。

在这个阶段，验证者发送一个随机采样的点 z∊F。证明者将 H₁(z²) 和 H₂(z²) 的求值连同计算 H(z) 所需相关元素的掩码的求值一起发回。用 {yⱼ} 表示证明者发送的这些值集。对于诚实的证明者，每个 yⱼ 的值等于 fₖ(zgˢ)，其中 k 是相应单元格的列，s 是其行偏移量。然后验证者可以通过两种方式计算 H(z)：基于 H1 和 H2（使用 H(z)=H1(z2)+z*H2(z2)）和基于掩码值 yⱼ。它验证两个结果是相同的。它还没证明证明者在这个阶段发送的值是正确的（即确实等于点 z 的掩码值），这将在下一节中完成。这种通过从一个大域中采样一个随机点来检查两个多项式之间一致性的方法称为DEEP（Domain Extension for Eliminating Pretenders）。感兴趣的读者可以在 DEEP-FRI 论文中找到更多细节。

DEEP 组合多项式

为了验证证明者发送的 DEEP 值是否正确，我们创建了第二组约束，然后将其转换为类似于上面定义的组合多项式的低度测试问题。

对于每个值 yⱼ，我们定义以下约束：

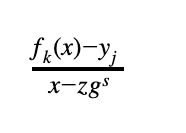
有理函数是度数 deg(fₖ)-1 的多项式当且仅当 fₖ(zgˢ) = yⱼ。用 M 表示掩码的大小。验证者从域中抽取 M+2 个随机元素 {𝛼ⱼ}ⱼ 。我们将用作为低度测试的多项式称为 DEEP 组合多项式。定义如下：

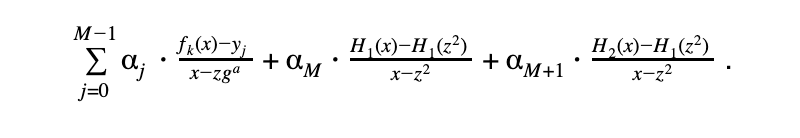
（注意，在第一项中，k 和 zgˢ 不是常数，而是取决于 j）。这是如下形式的（随机）线性组合：

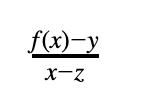
其中 f 是轨迹多项式或 H₁ / H₂ 多项式。因此，证明这种线性组合是低度的意味着证明轨迹多项式的低度以及 H 1 和 H 2 多项式的低度，以及 DEEP 值是正确的。

低度测试

低度测试的 FRI 协议

对于低度测试，我们使用称为 FRI（代表 Fast Reed-Solomon Interactive Oracle Proof of Proximity）协议的优化变体，感兴趣的读者可以在这里阅读更多相关信息。相关的优化在下文详述。

如我们关于该主题的文章所述，该协议由两个阶段组成：承诺阶段和查询阶段。

承诺阶段

在基本的 FRI 版本中，证明者将原始的 DEEP 约束多项式，这里表示为 p₀(x)，分成两个度数小于 d/2 的多项式，g₀(x) 和 h₀(x)，满足 p₀(x)=g₀ (x²)+xh₀(x²)。验证者采样一个随机值𝛼₀，将其发送给证明者，并要求证明者承诺多项式 p₁(x)=g₀(x) + 𝛼₀h₀(x)。注意，p₁(x) 的度数小于 d/2。

然后我们通过将 p₁(x) 拆分为 g₁(x) 和 h₁(x) 继续递归，然后选择一个值 𝛼₁，构造 p₂(x) 等等。每次，多项式的度数减半。因此，在 log(d) 步骤之后，我们得到了一个常数多项式，证明者可以简单地将常数值发送给验证者。

正如读者所预料的那样，上述多项式求值的所有承诺都是通过使用上述默克尔承诺方案做出的。

为了使上述协议起作用，我们需要一个性质：对于域 L 中的每个 z， -z 也要在 L 中的。此外，p₁(x) 上的承诺不会超过 L，但是超过 L²={x² : x ∊ L}。由于我们迭代地应用 FRI 步骤，L² 还必须满足 {z, -z} 属性，依此类推。通过我们选择使用乘法陪集作为我们的求值域来满足这些代数要求。

查询阶段

我们现在须检查证明者没有作弊。验证者对 L 中的一个随机 z 进行采样并查询 p₀(z) 和 p₀(-z)。这两个值足以确定 g₀(z²) 和 h₀(z²) 的值，从以下两个“变量”g₀(z²) 和 h₀(z²) 中的两个线性方程可以看出：

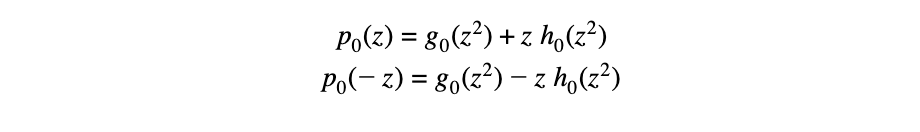
验证者可以求解这个方程组并推导出 g₀(z²) 和 h₀(z²) 的值。因此它可以计算 p₁(z²) 的值，它是两者的线性组合。现在验证者查询 p₁(z²) 并确保它等于上面计算的值。这表明证明者在承诺阶段发送的对 p₁(x) 的承诺确实是正确的。验证者可以继续，通过查询 p₁(-z²)（回想一下(-z²)∊ L² 并且 p₁(x) 上的承诺是在 L²) 上给出的，并从中推导出 p²(z⁴)。

验证者以这种方式继续，直到它使用所有这些查询最终推导出 P_h(z) 的值，当中 h=log(d)。但是，回想一下，P_h(z) 是一个常数多项式，其常数值是由证明者在承诺阶段（在选择 z 之前）发送的。验证者应检查证明者发送的值是否确实等于验证者从对先前函数的查询中计算出的值。

验证者收到的所有查询回应也需要与证明者在承诺阶段发送的默克尔承诺进行一致性检查。因此，证明者将解除承诺信息（默克尔路径）与这些回应一起发送，以允许验证者执行此操作。

此外，验证者还必须确保 p0 多项式与衍生出它的原始轨迹（fⱼ 和 Hⱼ）之间的一致性。为此，对于查询阶段的两个查询值 p₀(z) 和 p₀(-z) 之一，证明者还将由 DEEP 组合多项式归纳的 fⱼ 和 Hⱼ 的值连同它们的解除承诺一起发送。然后，验证者检查这些值与跟踪上的承诺的一致性，计算 p₀ 的值并检查它与证明者发送的值 p₀(z) 的一致性。

为了达到协议所需的健全性，查询阶段会重复多次。对于 2ⁿ 的放大系数，每个查询大致贡献了 n 位安全性。

转换为非交互式协议 (Fiat-Shamir)

到目前为止，上述协议被描述为交互协议。在我们的 Alpha 版本中，我们将交互式协议转换为非交互式版本，以便证明者以文件（或相等的二进制表示）的形式生成证明，验证者接收它以验证其正确性（链上）。

通过 BCS 构造来消除交互性，这是一种将交互式 Oracle 证明 (IOP)（例如上述协议）与密码哈希函数相结合以获得密码证明的方法。有关此机制的一些背景信息，请参阅我们的博客文章。

这种结构背后的基本思想是证明者模拟从验证者那里接收随机性。 这是通过从哈希函数中提取随机性来完成的，该哈希函数应用于证明者发送的先前数据（并附加到证明中）。这种结构通常被称为哈希链。在我们的 Alpha 版本中，哈希链是通过对证明者和验证者都知道的公共输入进行哈希来初始化的。为了简单起见，省略了进一步的技术细节。

证明长度优化

除了上述协议的描述外，我们还采用了几种优化技术来减少证明大小。这些技术将在以下小节中描述。

FRI 层跳过

在 FRI 协议的承诺阶段，证明者可以跳过 FRI 层并仅在其中的一个子集上承诺，而不是在每个 FRI 层上承诺。这样做，证明者减少了一些默克尔树的创建，这意味着在查询阶段它有更少的解除承诺路径发送给验证者。不过，这里有一个权衡。例如，如果证明者只是每三层承诺一次，为了回答查询，它需要在第一层的 8 个元素解除承诺（而不是在标准情况下发送的 2 个）。证明者在承诺阶段考虑了这一事实。它将默克尔树的每个叶子中的相邻元素打包在一起。因此，跳过层的成本是发送更多的域元素，而不是更多的身份验证路径。

FRI 最后一层

另一个用于减少证明大小的 FRI 优化是在最后一层达到常数值之前终止 FRI 协议。在这种情况下，证明者不会发送最后一层的常数值作为承诺，而是发送代表最后一层的多项式的系数。这允许验证者像以前一样完成协议，而无需承诺（并为较小的最后层中的域元素发送解除承诺）。在我们的 Alpha 版本中，FRI 承诺阶段通常在达到小于 64 次的多项式 pⱼ 时终止。确切的数字可能因轨迹大小而异。

Grinding

如上所述，每个查询都会为证明的安全性（健全性）添加一定数量的位。然而，这也意味着证明者会发送更多的解除承诺，这会增加证明的大小。减少查询需求的一种机制是增加恶意证明者生成虚假证明的成本。我们通过在上述协议中添加一个要求来实现这一点，即在证明者做出的所有承诺之后，它还找一个 256 位随机数与哈希链的状态一起哈希，生成所需长度的预定义模板。模板的长度定义了证明者在生成表示查询的随机性之前必须执行的一定量的工作。结果，试图生成有利查询的恶意证明者将需要在每次更改承诺时重复grinding过程。另一方面，诚实的证明者只需要执行一次grinding。

在我们的 Alpha 版本中，我们使用具有特定模式的模板，其中包含已执行grinding的位数和固定模式。这类似于在许多区块链上执行的grinding。证明者找到的 nonce 作为证明的一部分发送给验证者，然后验证者通过运行一次哈希函数来检查其与哈希链状态的一致性。

在我们的 Alpha 版本中，证明者需要执行 32 位grinding。因此，可以减少达到若干安全级别所需的查询数量。爆炸倍数为 2⁴，这允许将查询数量减少 8。

用于grinding的位数作为参数传达给验证者。如果证明与该参数不一致，验证者将拒绝该证明。

周期列

许多密码原语涉及使用一些列表常数。当我们多次应用相同的密码原语时，我们会得到一个周期性的常数列表。在 AIR 中使用此列表的一个选项是将其值添加到轨迹中并提供保证其值正确的约束。但是这造成浪费，因为验证者知道该列表的值，因此计算 LDE 并承诺它们是没有意义的。相反，我们使用一种我们称为周期列的技术。每个这样的列的周期结构产生可以简洁地表示的列多项式。在多项式的经典表示，a₀+a₁x+a₂x²+…aₙ*xⁿ ，其系数 (a₀,…,aₖ) 的向量的简洁表示意味着大多数 aⱼ 为零。这使验证者能够有效率地计算这些多项式的逐点求值。

总结

StarkDEX 系统使用的通用 STARK 证明系统的描述到此结束。 所描述的 STARK 证明系统保留了已知的好处，例如透明度（消除了受信任的设置）、高度可扩展的验证和后量子安全性。 最重要的是，它包括几个创新的贡献和优化，显着减少了证明的大小，并以以前文献中没有描述的方式增强了有效可证明陈述的表达能力。

在本系列的下一篇也是最后一篇文章中，我们将描述我们如何为 StarkDEX 构建 AIR（Algebraic Intermediate Representation）。与往常一样，如果您有任何问题或意见，请在此处或在推特 @StarkWareLTD 上与我们联系。

Kineret Segal & Gideon Kaempfer

StarkWare