算术化

许多零知识证明系统都使用算术化的方法，将计算类问题简化成涉及有限域F上的多项式的代数问题。zk-STARK对计算完整性（ Computational Integrity， CI）声明，“输出结果α是程序C根据输入x经过T步执行所得”，进行证明的第一步是算术化。

zk-STARK算术化的方法包括2个重要方法，首先，构建程序C的代数中间表达(Algebraic Intermediate Representation, AIR)，用s个多项式描述当前执行状态与下一步状态的转化约束；其次，为降低证明者的时间复杂度和空间复杂度，将上述多项式进行链接合并形成1个多项式，该方法称为ALI（Algebraic Linking Interactive Oracle Proof）。 详细说明如下。

AIR

对计算完整性进一步深入理解下，实际上需要通过AIR将这一约束表达出来，即从输入x到输出α的程序执行过程中的中间计算状态转换，中间计算状态则是一堆寄存器数值。因此，给出AIR的定义，是一个低度多项式的集合

$P=\{P_1(\overrightarrow{X},\overrightarrow{Y}),...,P_s(\overrightarrow{X},\overrightarrow{Y})\}$

1. 低度多项式的系数在域 $F$内
2. $\overrightarrow{X}=(X_1,...,X_w)$ 代表当前计算状态
3. $\overrightarrow{Y}=(X_1,...,X_w)$ 代表下一步计算状态
4. $w$ 是证明系统所中某一个计算状态的变量数量
5. $P_i$ 代表转换关系的多项式
6. 有一对解$(\overrightarrow{x},\overrightarrow{y})$使得转换关系成立，当且仅当 $(\overrightarrow{x},\overrightarrow{y})$是$P$的共同的解，即 $P_1(\overrightarrow{x},\overrightarrow{y})=...=P_s(\overrightarrow{x},\overrightarrow{y})=0$
7. AIR的多项式的度是 所有$P_i$中的最大值
8. s 是所有约束的数量

通过上述定义，可以看出，AIR将程序C执行过程中寄存器数值前后变化关系转化成了约束多项式，以便验证者能信任输入x到输出y的完整过程，而不是随便得出的结果或者是伪造的输出结果。

那么，上述的计算状态具体包括什么，如何组织，请查看执行轨迹

ALI协议

由于多项式的插值计算及验证计算需要耗费大量的计算资源，因此，ALI协议将s个多项式约束化简为单一约束，例如，可以使用随机线性组合。

实际上，采用ALI协议后，具有更好的可靠性(soundness)。如果对证明过程感兴趣，可以参考 Eli Ben Sasson 的文章Scalable, transparent, and post-quantum secure computational integrity附录D

执行轨迹（Execution trace 或者 trace）

执行轨迹是由执行某个计算时，一组机器状态序列构成。说得直白点，就是为了执行某个程序C，申请了W个寄存器，执行了N个步骤，那么执行轨迹可以用一张大小为$N\times W$表来描述。

以斐波那契数列计算为例，可参考ZKHack Mini2 Can you turn up the heat?

fn fib(start: (Felt, Felt), n: usize) -> Felt {
    let mut t0 = start.0;
    let mut t1 = start.1;

    for _ in 0..(n - 1) {
        t1 = t0 + t1;
        core::mem::swap(&mut t0, &mut t1);
    }
    t1
}

可以看到这里使用了2个寄存器，s0、s1分别存放每一个中间状态下的数据。模拟n = 10的时候，生成的执行轨迹是一个数组，包含了5对中间状态数据(state[0],state[1])。这里的执行轨迹是由prover定义并生成的，源码如下：

	pub fn build_trace(start: (Felt, Felt), n: usize) -> TraceTable<Felt> {
        
        let mut trace = TraceTable::new(2, n / 2);
        trace.fill(
            |state| {
                state[0] = start.0;
                state[1] = start.1;
            },
            |_, state| {
                state[0] += state[1];
                state[1] += state[0];
            },
        );

        trace
    }

执行轨迹中的数据如下图所示。

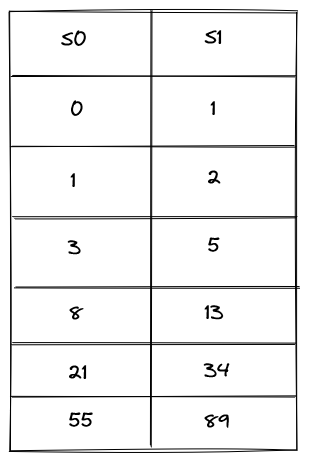
这样定义出来的执行轨迹只有2列，状态转换的具体约束条件如下：

		result[0] = next_state[0] - (current_state[0] + current_state[1]);
    result[1] = next_state[1] - (current_state[1] + next_state[0]);

也就是说，每一次状态转换必须满足这2个约束：

1. s_{0, i+1} = s_{0, i} + s_{1, i}
2. s_{1, i+1} = s_{1, i} + s_{0, i+1}

相应的约束多项式的度最大为1。因此，创建AIR时，定义状态转换的约束多项式的度为1。

		let degrees = vec![
            TransitionConstraintDegree::new(1),
            TransitionConstraintDegree::new(1),
        ];

此外，AIR中还需要对输入、输出进行约束，参考如下：

		vec![
            Assertion::single(0, 0, self.start.0),       // input contraint
            Assertion::single(1, 0, self.start.1),       // input contraint
            Assertion::single(0, last_step, self.end),   // output contraint
        ]

至此，我们就构建了执行轨迹，并根据执行轨迹构建了对应的约束。

实际上，构建一个合理执行轨迹，并据此设计无懈可击的约束系统是学习并使用ZK-Stark非常重要的一步。如果感兴趣，可以参考**ZKHack Mini1: There’s something in the AIR ** ，帮助更深入地理解AIR。

ZK-STARK 证明系统

STARK 中的多项式承诺

两种类型的多项式

从算术化的约束系统中，我们会得到两种类型的witness，第一是整个待证明程序的执行轨迹，也叫做execution trace，第二是在执行过程中需要满足的约束条件，称为 constraint。

执行轨迹可以看成是一组寄存器的状态转换过程。这里我们仍以斐波那契数列的计算为例，假设我们要求出 fib(10)，且用两个寄存器 s0, s1 来保存计算的中间状态，那么在程序正确执行5步后，s0[5] 就是我们需要的计算结果。

有了程序的执行轨迹，我们还需要额外的约束来保证执行轨迹确实是程序按照我们给出的计算方式来生成的。约束分为两部分：

1. 在边界处，寄存器的状态必须和指定的寄存器状态一致。例如 s0, s1 的初始状态要满足 s0[0] = 0 且 s1[0] = 1。另外，我们得到的计算结果必须是程序执行到第5步后 s0 寄存器的状态，即 result = s0[5]。
2. 寄存器每一次的状态转换必须满足如下计算规则：
   1. s0[i] + s1[i] = s0[i+1]
   2. s1[i] + s0[i+1] = s1[i+1]

有了这些约束，我们就能够信任程序的执行结果，即 fib(10) = result = s0[5] 了。接下来我们需要对执行轨迹和约束条件做多项式承诺。

承诺一个多项式

在讲具体的实现之前，我们先来了解 STARK 中是如何对一个多项式进行承诺的。我们知道一个多项式承诺方案（polynomial commitment scheme）需要满足如下使用场景：

1. 设置：能够生成特定的代数结构 $\mathbb{G}$，以及公私钥对 $⟨PK,SK⟩$ ，用于承诺一个度数小于 $t$ 的多项式
2. 承诺：输出多项式 $\varphi (x)$ 的承诺 $\text{C}$
3. 打开：对于验证者给定的 $i$，证明者给出多项式在该点处的值 $\varphi (i)$，以及关于该求值的一个证明。验证者能够利用之前的承诺 $\text{C}$ 验证其求值是正确的

在常见的 $KZG$ 多项式承诺方案中，证明者首先使用椭圆曲线点乘的方式，对多项式进行承诺，随后在打开时构造一个新的商多项式，使得验证者可以通过椭圆曲线配对，验证该商多项式正是原始的 $\varphi (x)$ 在挑战点处构造出的多项式。具体的步骤可以参考 $KZG$ 的论文，这里不再赘述。

STARK 使用默克尔树进行多项式承诺，实现方式如下：

1. 设置：STARK不需要额外的可信设置，但需要事先确定用于构造默克尔树的哈希函数
2. 承诺：首先求出多项式 $\varphi (x)$ 在其求值域上所有单位根处的值，$\varphi ({\omega }^0),\varphi ({\omega }^1),\varphi ({\omega }^i),...$，以这些值为叶子节点，组成一颗默克尔树，最后公开得到的默克尔树树根，即是该多项式的承诺。
3. 打开：验证者选定随机挑战点，证明者提供多项式在该点处的值，以及一条默克尔树路径。验证者检查该默克尔树路径合法。

轨迹多项式（Trace Polynomial）的承诺

对于任何一个 STARK 寄存器的执行轨迹，我们可以将它的每一行看作是其对应的轨迹多项式在某个单位根处的取值。因此，对于示例中的 $s0(x),s1(x)$，我们有：

$$\begin{gathered} s0({\omega }^0)=0,s1({\omega }^0)=1 \\ s0({\omega }^1)=1,s1({\omega }^1)=2 \\ s0({\omega }^2)=3,s1({\omega }^2)=5 \\ s0({\omega }^3)=8,s1({\omega }^3)=13 \\ s0({\omega }^4)=21,s1({\omega }^4)=34 \\ s0({\omega }^5)=55,s1({\omega }^5)=89 \end{gathered}$$

因为默克尔树要求叶子节点个数必须是2的幂次，这里我们需要补上程序继续按约束条件运行的结果：

$$\begin{gathered} s0({\omega }^6)=144,s1({\omega }^6)=233 \\ s0({\omega }^7)=377,s1({\omega }^7)=610 \end{gathered}$$

这样就可以为 $s0(x),s1(x)$ 分别生成默克尔树承诺了。不过请稍等，为了协议的安全性，我们还需要进行扩展。

低度多项式扩展（Low-Degree Extension）

从程序的执行轨迹中，我们得到了数个长度为 $N$ 的轨迹多项式。实际的使用场景里，出于安全性的考虑，我们需要在一个更大的求值域上承诺该多项式，一般需要将求值域扩大 $2^k$ 倍，扩大的倍数称为爆炸倍数（ blowup factor），该求值域称为 $LDE$ 域。

我们会在 DEEP-FRI 章节讨论安全性的问题。现在来看如何将长度为 $N$ 的轨迹多项式扩展到 $2^{k}N$ 。我们先利用拉格朗日插值法，求出该轨迹多项式的各项系数 $a_0,a_1,a_2,..,a_{n-1}$ （注意其单位根需要使用 $2^{k}N$ 求值域上的单位根），然后我们在 $2^{k}N$ 的求值域上用系数求出其他单位根处的多项式值。这种利用一个低次多项式生成更大的求值域上单位根处值的方法称为低度多项式扩展。

下图是 blowup factor = 2 时， $s0(x)$ 的低度多项式扩展示例，黄色的节点是多项式在原始的求值域上对应单位根处的值（它们也是在 $LDE$ 域上所有单位根处值的一部分，因为 ${\omega }_{origin}^i={\omega }_{LDE}^{2^k\ast i}$ ），蓝色为 $LDE$ 扩展后新的单位根处的求值：

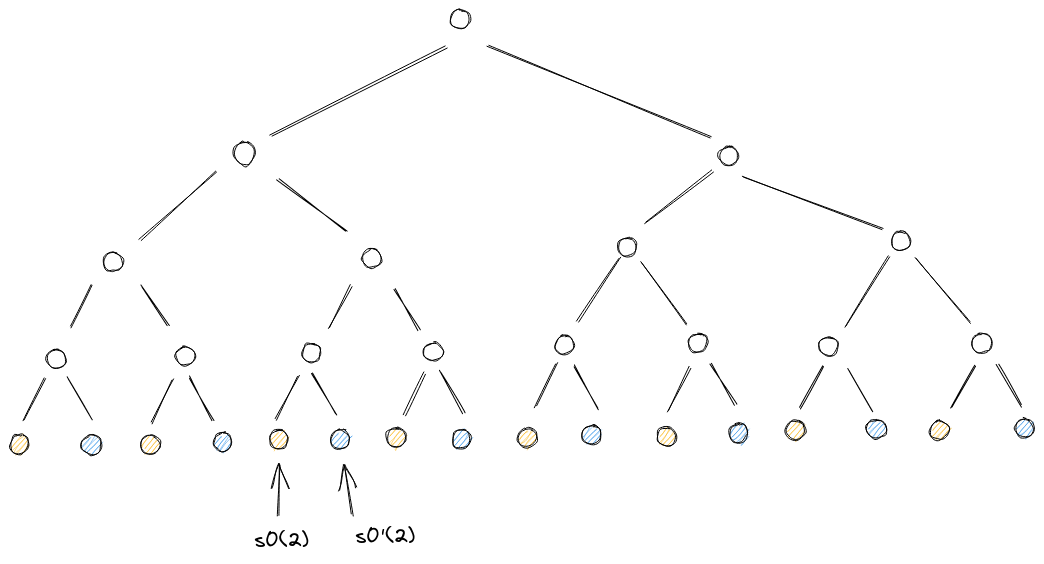
约束多项式（Constraint Polynomial）的承诺

程序在执行过程中需要满足的约束条件，同样也可以转换为多项式来表示。例如，我们要约束 $s0({\omega }^5)=55$，可以按如下的方式构造约束多项式：

$c(x)=\frac{s0(x)-55}{x-{\omega }^5}$

根据多项式基本定理，$s0(x)-55$ 可以被 $x-{\omega }^5$ 整除当且仅当 $s0({\omega }^5)=55$。也就是说，当约束条件满足的时候， $c(x)$ 的次数小于 $s0(x)$。我们利用这种方法，将所有的约束条件写成多项式的形式：

1. $c0(x)=\frac{s0(x)-0}{x-{\omega }^0}$
2. $c1(x)=\frac{s1(x)-1}{x-{\omega }^0}$
3. $c2(x)=\frac{s0(x)-55}{x-{\omega }^5}$
4. $c3(x)=\frac{s0(\omega x)-s0(x)-s1(x)}{{\prod }_{i\in [0,6]}x-{\omega }^i}$
5. $c4(x)=\frac{s1(\omega x)-s0(\omega x)-s1(x)}{{\prod }_{i\in [0,6]}x-{\omega }^i}$

将约束多项式组合起来

如果一个个检查约束多项式的次数，代价会很大，也没有必要。我们可以将所有的约束多项式组合到一起，形成一个组合多项式（Composition Polynomial），对该组合多项式的检查即是对所有约束多项式的检查。

在组合之前，有一点要注意：上述的约束多项式的次数不是相同的。需要先将约束多项式补齐到相同的次数，然后再组合。补齐的方法是将它乘上一个随机的 $D-D_j$ 次多项式，该随机多项式的系数是验证者在证明者承诺完轨迹多项式后随机产生的。

$CP(x)={\sum }_{j=0}^4{c}_j(x)(\alpha x^{D-D_j}-{\beta }_j)$

最后我们得到 组合多项式 $CP(x)$，别忘了我们需要在 $LDE$ 域上承诺它，因此也要像之前的轨迹多项式那样，使用低度多项式扩展的方式进行承诺。

DEEP-FRI

得到轨迹多项式和组合多项式后，其实我们已经可以进行证明了。只要把轨迹多项式和组合多项式再做一次随机的线性组合，然后证明最终的多项式度数小于 $D$ ，就能证明所有的约束条件满足，且程序的执行过程和被承诺的Trace一致。

但是，从安全性角度出发，还需要做一些调整。STARK 使用称为 Domain Extension for Eliminating Pretenders (DEEP) 的方法进行检查。我们需要从基域上随机选一个点，然后检查在这个点上，各多项式的值是否满足约束。基域是自变量 $x$ 的取值范围 $\mathbb{F}$ ，是一个比 $LDE$ 域大得多的域。

设我们挑选了随机点 $z\in \mathbb{F}$ ，则 $DEEP$ 多项式可以构造为：

$DEEP(x)={\alpha }_0\frac{s0(x)-s0(z)}{x-z}+{\alpha }_1\frac{s1(x)-s1(z)}{x-z}+{\alpha }_2\frac{CP(x)-CP(z)}{x-z}$

在实际应用中，$CP(x)$ 的度数一般比轨迹多项式要高，取决于约束条件。如果约束条件有两列相乘（即二次的约束），则 $CP(x)$ 的度数就为 $2D$ 。这种情况下，需要将 $CP(x)$ 拆分为多个次数小于 $D$ 的多项式。本文中因为约束是一次的，因此 $CP(x)$ 的次数和轨迹多项式的次数一致。另外，上面构造的 $DEEP(x)$ 多项式，正常来说其次数应该小于 $D-2$ （因为分子均为次数小于 $D-1$ 次的多项式，而分母为 $1$ 次多项式）。但为了后面做 FRI 承诺的时候计算方便，我们仍然通过乘上一个多项式的方式，将其次数升高一次，这样它的次数应该小于 $D-1$ 。

关于构造 $DEEP(x)$ 多项式的必要性，可以参考 Eli Ben Sasson 的文章 DEEP-FRI: Sampling Outside the Box Improves Soundness

构造完 $DEEP(x)$ 后，如果能够证明 $DEEP(x)$ 是一个次数小于 $D-1$ 的多项式，就可以证明所有的多项式在 $z$ 点处的取值即是所预期的值，进而证明程序的执行结果正确，且所有的约束条件都满足。

FRI 低度多项式测试

低度多项式测试的原理

怎样证明一个多项式 $f(x)$ 的次数小于特定的 $D$ 次呢？低度多项式测试提供了一种方法，即：从 $f(x)$ 上任意挑选 $D+1$ 个点值对 $(x_i,f(x_i))$，使用其中的 $D$ 个点值对构造一个 $D-1$ 次多项式 $f^{\prime }(x)$ 。若 $f^{\prime }(x)$ 和 $f(x)$ 在第 $D+1$ 个点处的求值相等，则有较大的概率 $f(x)$ 是一个次数小于 $D$ 的多项式。

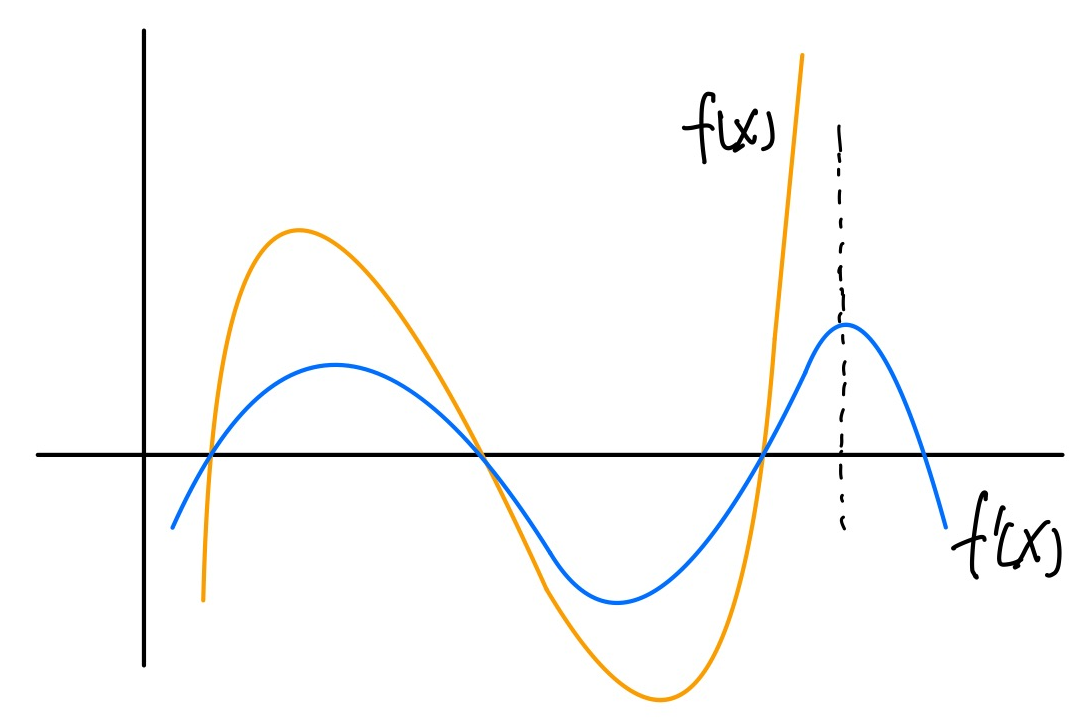
出于安全性的考虑，可以将这个过程重复 $k$ 次。若进行一次测试，证明者作弊成功的概率为 $p$，那么挑选 $D+k$ 个点值对，证明者成功的概率就是 $p^k$ 。

使用折叠减小开销

上述低度多项式测试的方法有一个缺点，即构造 $f^{\prime }(x)$ 需要 $D+k,k\ge 1$ 个点值对，在多项式度数非常大的前提下，测试需要的时间和通信量也会变得无法承受。FRI 通过一种称为“折叠”的方法，降低了通信开销。具体做法是：

1. 首先将所有的 $n$ 个点值对 $(x_i,f(x_i))$ 按 $N$ 列进行划分，得到一个 $\frac{n}{N}$ 行，$N$ 列的矩阵
2. 证明者需要承诺矩阵的每一行，承诺的方式是将一行中所有的 $f(x_i)$ 进行哈希，得到共$\frac{n}{N}$ 个哈希值，组成默克尔树并输出树根
3. 对应每一行，证明者将该行的所有点值对使用随机数 $\alpha$ 进行线性组合： $f^{\prime }(x_i^{\prime })=f(x_i)+\alpha f(x_{i+1})+...+{\alpha }^{j}f(x_{i+j})+...+{\alpha }^{N-1}f(x_{N-1})$
4. 注意到，如果我们精心挑选 $x_i$，则得到的新多项式可以看成原多项式的每一项按模 $N$ 划分出的多项式的组合，其系数正是原多项式对应项系数的线性组合
5. 这样我们得到了一个项数为 $\frac{n}{N}$ 的多项式 $f^{\prime }(x)$ ，再次重复1-4步，直到我们将新多项式的次数降到可以承受的范围之内。
6. 假设我们重复了 $k$ 次，则只需检查最后的多项式次数是否小于 $\frac{D}{N^k}$ 即可

第4步的解释：

我们构造的新 $f^{\prime }(x_i)$ 可以看成是 $N$ 个多项式的线性组合，假设原来的多项式的求值域上单位根分别为 ${\omega }^0,{\omega }^1,{\omega }^2,...,{\omega }^n$ ，那么新的多项式其求值域是原来的 $1/N$ ，其单位根变为 ${\omega }^0,{\omega }^N,{\omega }^{2N},...,{\omega }^{\frac{n}{N}\ast N}$

$f^{\prime }({\omega }^0)=f({\omega }^0)+\alpha f(w^0\ast w^1)+{\alpha }^{2}f({\omega }^0\ast {\omega }^2)+...$

$f^{\prime }({\omega }^N)=f({\omega }^N)+\alpha f(w^N\ast w^1)+{\alpha }^{2}f({\omega }^N\ast {\omega }^2)+...$

$f^{\prime }({\omega }^{2N})=f({\omega }^{2N})+\alpha f(w^{2N}\ast w^1)+{\alpha }^{2}f({\omega }^{2N}\ast {\omega }^2)+...$

令 $u(x)=f(x\ast \omega ),v(x)=f(x\ast {\omega }^2),w(x)=f(x\ast {\omega }^3),...$ ，则有

$f^{\prime }(x)=f(x)+\alpha u(x)+{\alpha }^{2}v(x)+...,x\in [{\omega }^0,{\omega }^N,...]$

可见 $f^{\prime }(x)$ 是次数为 $\frac{n}{N}$ 的多项式

验证者的检查

检查FRI步骤的正确性

首先，因为证明者每次 FRI 折叠的时候都承诺了折叠后所有新点值对的默克尔树，验证者只需在同一层上抽取 $N$ 个相关的折叠点，在下一层上抽取一个点，就能验证本层的 $N$ 个点确实按正确的随机数折叠到了下一层的同一个点。

其次，验证者检查最后余下的多项式是否满足度数小于 $\frac{D}{N^k}$ ，这个使用低度多项式测试进行抽查即可验证。

检验多项式是否匹配

事实上，证明者如果伪造一个 $DEE{P}_{fake}(x)$ ，它的度数小于 $D$ ，那么它总是能够通过低度测试。 因此验证者需检查：通过 FRI 低度测试的多项式，确实为证明者构造的 $DEEP(x)$ 多项式。验证者可以向证明者请求 $LDE$ 域中任意一点处的 $DEE{P}_{fake}(x)$ 的值，以及之前的轨迹多项式，组合多项式在该点处的值 $s0(x),s1(x),CP(x)$ 。验证者自行计算 $DEE{P}_{real}(x)$ ，若它和证明者发送的 $DEE{P}_{fake}(x)$ 不匹配，则验证不通过。

如果证明者想要伪造 $DEE{P}_{fake}(x)$ ，他需要让该多项式的度数小于 $D$ 。因此若原始的 $DEE{P}_{real}(x)$ 是个高次多项式（次数很高，远高于 $LDE$ 求值域的度数），则二者在 $LDE$ 上最多可以在 $D$ 个求值点处相等（若有多于 $D$ 个求值点相等，则伪造的多项式 $DEE{P}_{fake}(x)$ 次数必定大于等于 $D$ ）。此时，验证者随机检查一个求值点，两个多项式在点处值相等的概率即为 $1/2^k$ （ $k$ 为爆炸倍数）。验证者可以多次重复这一过程，直到证明者作弊成功的概率小于目标安全参数即可。

ZKHack-Mini 上有一个证明者通过伪造 $DEEP(x)$ 进行攻击的例子，可以参考 ZKHack-Mini: Puzzle 2 。

磨损因子(Grinding Factor)

因为上述的验证手段均为概率的，为防止证明者靠庞大的计算能力进行反复重试，可以要求证明者在提供 STARK 证明的同时也提交一个工作量证明 （PoW），使得重试的代价变大。

参考文献

StarkDEX Deep Dive: the STARK Core Engine

ethStark

Vitalik STARK series I: Proofs with Polynomials

Vitalik STARK series II: Thank Goodness It's FRI-day

Vitalik STARK series III: Into the weeds

DEEP-FRI: Sampling Outside the Box Improves Soundness

ZKHack

ZK-STARK 如何工作及其安全性

关于其证明系统，ZK-STARK证明系统已经有详细的描述，这里不再赘述。本文主要记录下STARK系统的基础和安全性的简单讨论。

1. 安全性和 bit 安全性

下面这段描述引用自 >When we say that a cryptographic system has a security level of λ bits, we mean, somewhat informally, that the best known attack on it requires running time ≥ $2^{\lambda }$^[1]

从中我们就可以明白，密码学中的所谓的“security strengh(security level)”就是在已知最好的破解方法下，需要多少时间能够破解。只不过这里的“时间”，是用算法需要进行尝试的次数来估计的。于是，“bit security level”就是这个次数的二进制表示而已。

安全性有以下几点需要注意：

• $\lambda$ bits并不代表就有 $2^{\lambda }$ 的计算机指令。具体的指令数目是由具体的硬件和指令集有关。
• 特别在公钥密码中，key bits的长度不一定就代表了bit security level。具体是与攻击方法有关的。比如： 2048-bit RSA就不具备2048 bits security level， 这是因为它的攻击方法是大质因数分解问题的复杂度。

2. FRI 的基本原理

概括来说，本质上，STARK最终是利用FRI证明了某一个多项式的次数是小于一个固定界限的，也就是所谓低度测试(Low-Degree-Testing)，而这个多项式表示了待证问题的计算过程。所以讨论STARK协议的安全性，可以等同于讨论FRI的安全性。

2.1 RS Proximity Testing/Verification

之所以简单介绍RS code， 是因为FRI论文就是为了解决RS proximity testing问题而提出的。同时，RS code是一组编码方法，它本质是一种 纠错码，最开始是为了解决通信中由于通信信道不可信导致的接收方来检测和更正发送方发来的原始数据的。它的基本思想很简单，就是通过发送方按照算法发送 冗余 来达成目的。

2.1.1 Original RS Code(RS60)

在FRI文献中所找到的RS60，就是指 I. S. REED 和 G. SOLOMON在1960年发表的《POLYNOMIAL CODES OVER CERTAIN FINITE FIELDS》^[2]论文所提出的纠错码编码方法，因而得名RS code。这种编码方法，其实很容易理解，它有如下几个要点。

• 它的目的是将一个 $m$ 长度的消息(message)编码成一个固定长度 $n$ 的消息(codeword)
• message与codeword的具体表示都是定义在一个域上的，通常是 $GF(2^k)$。这里可以把它简单理解为就是字符串的二进制表示，一般 $n=2^k$。
• 编码方法很简单，它首先构造了一个 $(m-1)$ 次多项式，这个多项式的系数就是待编码的消息(message)；而编码的结果(codeword)就是这个多项式在某个乘法子群各点处的值。

正式的过程是：

1. message: m-tuple $(a_0,a_1,...,a_{m-1})$
2. 构造一个 $(m-1)$ 次多项式 $P(X)$, 使得 $P(X)=a_0+a_{1}x+a_2{x}^2+...+a_{m-1}{x}^{m-1}$
3. 在本原根处求值，形成 codeword $$\begin{array}{rl}& P(0)=a_0\\ & P(\beta )=a_0+a_1\beta +a_2{\beta }^2+...+a_{m-1}{\beta }^{m-1}\\ & P({\beta }^2)=a_0+a_1{\beta }^2+a_2{\beta }^4+...+a_{m-1}{\beta }^{2(m-1)}\\ & ......\\ & P({\beta }^{2^n-2})=a_0+a_1{\beta }^{2^n-2}+a_2{\beta }^{2(2^n-2)}+...+a_{m-1}{\beta }^{(m-1)(2^n-2)}\\ & P(1)=a_0+a_1+a_2+...+a_{m-1}\end{array}$$

所以最终的 codeword 就是 $(P(0),P(\beta ),P({\beta }^2),...,P({\beta }^{2^n-2},P(1)))$。

接收者在接到codeword之后如果发生错误的位置在一定范围内，接收者是可以从接收到的codeword“恢复”出正确的数据的。这是因为上面任意 $m$ 个方程都是线性无关的，所以只要“正确”的值还占主要地位，就可以恢复出正确数据。

目前RS Code已经是一族编码方法，后面的一个改进就是将原始的消息也放到codeword中。由于与主题关系不大，就不介绍了。

2.1.2 RS code相关概念

以下内容撷取、综述于Block code Wiki

1. message length： 这个容易理解，记为 $m$。
2. block length: codeword的长度，记为 $n$。
3. Rate $R$: $R=m/n$
4. distance： 就是两个不同的codeword之间各个位置上不同的code的个数。并定义下面的最小距离 $d$，以及相对距离 $\delta$ $$\begin{array}{rl}& d:=\underset{\genfrac{}{}{0ex}{}{m_1,m_2\in {\Sigma }^k}{m_1\ne m_2}}{\min }\Delta [C(m_1),C(m_2)]\\ & \delta =d/n\end{array}$$ 下面讨论RS Code的 $d$ 的值。任何两个不相等的 $(m-1)$ 次多项式至少有 $(m-1)$ 个交点， 所以任意两个codeword之间的距离至多是 $n-(m-1)$ 。同时存在两个codeword是有 $(m-1)$ 个交点，所以 $d=n-(m-1)=n-m+1$。

进一步有， $$\begin{array}{rl}& \delta =d/n\\ & =(n-m+1)/n\\ & =1-m/n+1/n\\ & =1-R+o(1)\end{array}$$

2.1.3 RS Code相关定义与符号

单列本小节是因为FRI论文中大量采用，为方便以及精确起见，介绍于此。以下将对上述RS Code做一个形式化定义，该形式化引用自Relation between degree and Hamming distance, 该引用虽然是一个论坛问答，但是综合FRI论文中的定义，认为其定义是合理的，故直接采用。

Let F be a finite field. Let $S\subset F$ be some non-empty set. Define the relative Hamming distance between two function $f,g:S\to F$ by $${\Delta }_S(f,g):=\frac{1}{|S|}|\{s\in S:f(s)\ne g(s)\}|$$. Fix some $0<\rho <1$. Let $RS[F,S,\rho ]$ be the set of functions on $S$ who are evaluations of polynomials of degree $<\rho |S|$: $$RS[F,S,\rho ]:=\{f:S\to F:\exists p\in F[x^{<\rho |S|}],f=p{|}_S\}$$. For a function $f:S\to F$, let $$\delta (f):={\Delta }_S(f,RS[F,S,\rho ])=min\{{\Delta }_S(f,g):g\in RS[F,S,\rho ]\}$$

该定义直接定义了两个多项式（函数）的Hamming distance, 以及最重要的 $RS[F,S,\rho ]$ 与 $\delta (f)$。简单来说，$RS[F,S,\rho ]$ 是一个多项式的集合，并且多项式的次数都是 $<\rho |S|$ 的，而 $\delta (f)$ 则是 $f$ 与所有次数小于 $\rho |S|$ 的相对Hamming distance的最小值。

这里有一个需要注意的，不要受到前面介绍RS60的影响，这里的 $S$ 并不是原始消息(message)，而是对求多项式进行求值的定义域（即 $0,\beta ,{\beta }^2,...,$）。

2.1.4 RS proximity problems 和 RS proximity testing/verification

The RS proximity problem assumes a verifier has oracle access to $f:S\to F$, and asks that verifier to distinguish, with “large” confidence and “small” query complexity, between the case that $f$ is a codeword of $RS[F,S,\rho ]$ and the case that $f$ is $\delta$-far in relative Hamming distance from all codewords^[3]

所谓 proximity 问题就是一个概率问题，就是采取可接受的步骤，让verifier能区分出 $\delta (f)$ 是到达了预设的界限 $\delta$。

为了解决 RS proximity problems，有两大方法，一个是testing，一个是verification。二者的区别是，testing方法中prover提交证明后，不需要再提供额外的信息(意即verifier也不会再有额外的query)；而verification需要verifier多次query。而verification又分为，PCP model 和 IOPP model，区别是后者有多轮证明和多轮query。

最后，FRI 就是一种基于 IOPP model 解决RS proximity problems的一个方法。

2.2 FRI 与 DEEP FRI

2.2.1 FRI 折叠

FRI的核心是对欲承诺的多项式进行“折叠”，通过“折叠”将一个次数很高的多项式，逐步转化为次数较低，verifier可以接受的计算复杂度来验证的多项式。最后将结果多项式的系数发给verifier，verifier自己验证其次数。进而可以证明原始多项式的次数界限。

关于“折叠”的过程，ZK-STARK证明系统已经有较详细的阐述，这里只是换一种表达方式（论文方式），抛开复杂的数学符号和形式化的协议阐述，这里直接引用论文^[3]中的例子，并直接运用上文提到的一点点数学表示，就可以很清楚明白。

\begin{aligned} & prover \ claims:\ f^{(0)} : L^{(0)} → F \ is\ a\ member\ of\ RS[F,L (0) ,ρ] \ & i.e\ f^{(0)}\ is\ the\ evaluation\ of\ an
unknown\ polynomial\ P^{(0)} (X) ∈ F[X],\ deg(P) < ρ2^{n}\ \end{aligned}

很显然这是一个次数极高的多项式，于是做了如下变形：

$$\begin{array}{rl}& \forall x\in L^{(0)}{f}^{(0)}(x)=P^{(0)}(x)=P_0^{(1)}(x^2)+x\cdot P_1^{(1)}(x^2)\\ & letting{Q}^{(1)}(X,Y)\triangleq P_0^{(1)}(Y)+X\cdot P_1^{(1)}(Y)\\ & anddefining{q}^{(0)}(X)\triangleq X^2\end{array}$$

说的简单点就是按照类似于FFT的方法，对原多项式进行了变形，当然这里还有些其他推导，不过也不影响对主体过程的理解。

\begin{aligned} & verifier \ samples\ x^{(0)} ∈ F\ uniformly\ at\ random \ & and\ requests\ the\ prover\ to
send\ as\ its\ first\ oracle\ a\ function \ & f^{(1)} : L^{(1)} → F \ &that\ is\ supposedly\ the\ evaluation\ of \ & Q^{(1)}(x^{(0)} ,Y)\ on\ L^{(1)} . \end{aligned}

可以很清楚看到，$f^{(1)}$ 已经是 $<\frac{1}{2}\rho 2^n$ 的多项式。那么相对的，如果能证明 $f^{(1)}$ 的次数是小于 $\frac{1}{2}\rho 2^n$ 的那么也就证明了 $f^{(0)}$ 的次数是小于 $\rho 2^n$ 的。

以上就完成了一次“折叠”，prover的工作就是commit这些多项式，一直到最后一轮，最后一轮就直接把多项式发出来即可。

与之对应，verifier则需要针对该过程做两个检查：

• 确定最后一轮的多项式的次数
• 检查每一轮之间的约减是合法的(round consistency testing)。针对这个例子，采取的方法就是，所谓的 3-query test。以下是对该方法的综述。

$$\begin{array}{rl}& 1.sampleapairofdistinctelements{s}_0,s_1\in L^{(0)}suchthat{s}_0^2=s_1^2=y\\ & 2.query{f}^{(0)}(s_0),f^{(0)}(s_1)and{f}^{(1)}(y)denotethequeryanswersby{\alpha }_0,{\alpha }_{1}and\beta ,respectively\\ & 3.\because s_0\ne s_1,\therefore (s_0,{\alpha }_0),(s_1,{\alpha }_1)candetermineauniqueline,thisinpterpolatesthe{P}_Y^{(0)}(X)\\ & 4.check{f}^{(1)}(y)=P_Y^{(0)}(x^{(0)})\end{array}$$

这里有三点需要注意，

• 最后一步的左边是 $f^{(1)}(X)$，是verifier发给prover $x^{(0)}$之后确定的；而verifier自己插值出来的是 $P_Y^{(0)}(X)$。在正确的情况下，这两个多项式是 $Q^{(1)}(X,Y)$ 分别在固定 X， Y 时形成的。
• 该例中采用的是 $Y=X^2$，这是一个 $2-to-1$ 的一个映射，对定义域来讲完成了一个二分，就是分为两个coset（这就是论文反复提到的coset）。同时从值域角度来讲，也是将原来的求值域（也就是定义域）缩减到原来的一半，同时这也是下一轮的定义域。
• 个人理解所谓 3-query 是针对这个具体例子的。其代表的是verifier具体请求的点的个数，这里就是3个值，完成验证。如果有其他的“拆分”方法，query的个数也应该会不同。

2.2.2 FRI 协议

上面是“折叠”时，prover和verifier所做工作的一个示例。正式协议中，

• COMMIT PHASE 就是上述过程进行到最后一轮
• QUERY PHASE 最重要的一点是，round consistency testing要进行多次，这是为了提高协议的soundness lower bound，增强鲁棒性。

2.3 DEEP FRI

文献[4][5]主要都是在探讨（个人理解）怎样提高一种特定编码方式的lower bound(soundness)，只不过[4]在具体到RS问题时，对原始协议[3]并没有修改，其结果在[3]中的应用是改善了原协议的soundness，可以理解对原来bound分析的更精确化；而[5]则是在[4]的基础上进一步提高了soundness，提出了DEEP（Domain Extension for Eliminating Pretenders）方法，其在[3]上的应用，则是要对[3]的协议做出修改。

下图取自论文：

这两篇文献的特点都是讨论其方法在一般情况下的定理和性质，然后再具体到类似RS Code这种具体情况中。所以在查看论文时，如果不在意具体的对相关结论的铺陈和证明，则只需要关心其所要解决的问题，采用的方法和最后结论即可，只不过直接读论文，对这三点的掌握有可能淹没在茫茫公式中。

同时，直接查看 DEEP-FRI 或者是 ethSTARK，DEEP 方法的出现个人认为还是有点匪夷所思，所以以个人理解记录如下。

文献[4][5]总体来说都在讨论仿射结构 $u_x=u^{\ast }+x\ast u$ 与线性空间 $V$ 的平均距离和最大距离的关系。那么一个方向时在 $u^{\ast },u$ 与 $V$ 的距离是 $\delta$ 时，$u_x$ 与 $V$ 的距离；另一个方向就是 $u_x$ 与 $V$ 的距离为 $\delta$ 时， $u^{\ast },u$ 与 $V$ 的距离。

由于文献[4]作为过渡文献，虽然讨论的内容其实是很重要，但是其结果并未在 ethSTARK 中直接体现，更关键的是，它对于原本的 FRI 协议并未做修改，所以这里就直接简单记录下 DEEP 方法。

2.3.1 DEEP method for RS Code

弄清楚以下几点就可以明白该定理的含义：

• $V$ 是一大堆次数小于 $\rho |D|$ 的多项式的合集
• $V_{z,b}$ 是 $V$ 中在 $z$ 处值为 $b$ 的多项式的集合
• 图中(7)应该是一个条件，它描述了 $u^{\ast }+x\ast u$ 与集合 $V_{z,B_z(x)}$ 的距离在某一 $\delta$ 之内的概率，注意由于 $q$ 很大， $q>>d$ 且 $L_{\delta }^{\ast }$ 很小 这个概率值是很小的。翻译成普通话可以理解为，$u^{\ast }+x\ast u$ 所代表的多项式只要有可能是一个在 $z$ 处的值是 $B_z(x)$ 的次数小于 $\rho |D|$ 的多项式。
• $B_z(X)$ 的理解。设 $u^{\ast },u$ 代表的多项式分别为 $P^{\ast }(X),P(X)$，其在 $z$ 处的值为 $P\ast (z)={\alpha }^{\ast },P(z)=\alpha$。令 $B(Y,X)=P\ast (Y)+X\ast P(Y)$，则当 $Y=z$ 时， $B_z(X)=P\ast (z)+X\ast P(z)$ 就是一个一次多项式，当 $X=x$ 时就是具体的值 $B_z(x)$。虽然这是该定理的逆过程（该定理直接写出多项式$B$)，但是还是有助于理解，定理表达的就是一个高次多项式与 $B$ 相交于一个点。
• 由于 $v^{\ast },v\in V$ 的存在以及它们与 $u^{\ast },u$ 在 $C$ 上的值相等，那么结论就是 $u^{\ast },u$ 都是次数小于 $\rho |D|$ 的多项式。

通俗来说，只要 $u_x$有可能是一个在大域($Fq$) $z$ 处取值为 $b$ 的，次数小于 $\rho |D|$ 的多项式，那么它的两个组成部分 $u^{\ast },u$ 的次数也就都是小于 $\rho |D|$ 的。

2.3.2 DEEP-FRI

有了上述定理的铺垫，就能理解 DEEP-FRI 了，所谓 DEEP-FRI 就是采用了 DEEP 方法的 FRI。我的理解是，

$$\begin{array}{rl}& f^{(i)}代表第i轮的待证多项式\\ & H_x[f^{(i)}](Y)=P_0^{(i)}(Y)+x\ast P_1^{(i)}(Y)\\ & 如果H_x[f^{(i)}](Y)能够以一定的概率是小于d^{(i+1)}次的，那么P_0^{(i)}(Y)，P_1^{(i)}(Y)也都是小于d^{(i+1)}次的。\\ & 那么f^{(i)}就是小于d^{(i)}次的。\end{array}$$

上面这个想法就是 FRI，而 DEEP 会在接下来的过程中有所差异，原始 FRI 就此一直递归下去，而 DEEP 则是：

$$\begin{array}{rl}& DEEP方法要求证明H_x[f^{(i)}](X)是在z^{(i)}处的值为B_{z^{(i)}}(x^{(i)})的小于(d^{(i)}{)}^{{}^{\prime }}次多项式。\\ & 于是构造商多项式\\ & Quotient(H_{x^{(i)}}(X),z^{(i)},B_{z^{(i)}}(x^{(i)}))\\ & =\frac{H_{x^{(i)}}(X)-B_{z^{(i)}}(x^{(i)})}{X-z^{(i)}}=f^{(i+1)}\\ & 问题就转化成了证明f^{(i+1)}的次数d^{(i+1)}<(d^{(i)}{)}^{{}^{\prime }}-1\end{array}$$

有了以上思路整理，就可以明白 DEEP-FRI 协议了，下图取自[5]：

与之相应，协议对 round consistency testing 也有所调整。

note： $d^{(i+1)}=\frac{d^{(i)}}{2}-1$

2.3.3 DEEP ALI

这部分描述可能比较抽象，所以结合了 ethSTARK 的具体，看起来就明白了。下图取自论文[5]:

关于这段话，掌握以下三个要点：

• $f$ 是什么？答：可以理解为 ethSTARK 中的 $trace$ 多项式，就是 $witness$ 多项式
• $g$ 是什么？答：就是由 $f$ 构成（表示）的 $constraints$ 多项式。
• 有哪些事关 $g$ 的满足性的测试？答：一是 $g$ 本身是一个低度多项式，这是与 $g$ 本身的构造有关；二是，$g$ 确实是由先前提供的 $f$ 所组成的，这也就是文中所谓 consistency test。

标准做法就是 verifier 选择一个随机点 $\alpha$，要求提供（或者访问 oracle）所有相关 $f_i(\alpha \ast g^s)$ 的值（就是 $constraints$ 多项式各个组成部分在 $\alpha$ 处的值），以及 $g(\alpha )$，然后按照规则利用 $f_i(\alpha \ast g^s)$ 值计算 $g_{Verifier}(\alpha )$，然后检查 $g(\alpha )\stackrel{?}{=}{g}_{Verifier}(\alpha )$。上文指出这种方式 soundness 较低。（文中所说 $gap=\gamma \le \frac{1}{8}$，这里的 $\gamma$ 就是相对距离 $\delta$，$\delta$ 小，那么 soundness 就低，这是因为这说明两个多项式比较接近，只有少数不同，那算法检测出来的概率就低；理解这个还有一个关键，$\delta$是低度测试算法的输入，是事先就定好的，并且通常跟$\rho$有关）

DEEP 方法是，截图取自[5]：

简单说就是

• 把约束多项式做一个线性组合，产出 $g$。 (1 - 3)
• 将以前的随机点由 $\alpha$ 换成 $z$，注意，区别是 $z$ 是从一个比原来的求值域大得多的域上取来的。(4)
• 仍然分别求 $f,g$ 在 $z$ 处的值，并检查是否相等。(5)
• 对 $f,g$ 分别构造商多项式，这里说说我的理解。这是因为 $z$ 并非取自原有的求值域，所以不能在 commit 中直接检查 $f,g$ 在 $z$ 处的值是否正确，因此构造商多项式来证明。(6)
• 对商多项式进行低度测试。如成立，则证明了 (6) 的取值合法，又由于 (4) 则证明了 $f,g$ 的取值对应关系成立。还有一点，个人理解，对 $f,g$ 的商多项式的低度测试本身也证明了 $f,g$ 的本身是低度多项式（论文定理5.3^[5]），特别是 $g$ 多项式的低度测试，证明约束的满足。

2.3.4 DEEP 方法

从上面的讨论和总结来看，DEEP 方法本身不是什么高深莫测的方法，其要义是要对待证多项式在比原求值域大的多的域上，verifier 选取一个随机点 $z$，要求 prover 提供该处待证多项式的值，然后要求提供相应的商多项式的低度测试证明。它的功能有三个：

• 证明 prover 提供的点值确在某一多项式上
• 该多项式是次数低于某一次数的多项式
• 提高了以上两项证明的 soundness

从中也体会了文献[5]标题的含义，DEEP-FRI: Sampling Outside the Box Improves Soundness。

3. STARK 协议及其安全性

3.1 STARK 协议综述

目前 ethSTARK^[1] 就是基于 DEEP-ALI 的一套证明系统，该系统已经在ZK-STARK证明系统已经详细介绍。所以这里只做几个要点概述：

• 为什么需要 LDE？答：从前文对 RS Code 的介绍，在处理 RS Code 的问题时，相当于为了纠错而扩大了多项式的求值域。而在我们的场景下，是为了增强安全性，以降低 prover 在接受verifier 的检查时，“猜对”的概率。
• LDE 发生在何时？ 答：所有该承诺的多项式的commit值的求取，都应该发生在 LDE 域上（evaluation domain）；此外还有 FRI。
• 什么是 blowup factor？答：就是 RS Code 中的 R 的倒数，也就是 $\rho$ 的倒数。
• 除 FRI 外，哪些多项式需要 commit？答：所有的 $trace$ 多项式，以及 $Composition$ 多项式。注意 $Composition$ 多项式可能因为出现高次面临拆分。此时，其拆分出来的各个部分与 $trace$ 多项式次数相同，因此称为 $CompositionPolynomialTrace$，它们需要分别进行与 $trace$ 多项式相同的 LDE，然后进行 commit。
• commit的方式是什么？有何优化？答：方式是 Merkle Tree。优化是所有 $trace$ 多项式组成一棵 Merkle Tree，其叶子是各 $trace$ 多项式在同一点求值（所谓同一个 row）的拼接。$CompositionPolynomialTrace$ 亦然。
• 什么是 Compostion 多项式？答：就是约束多项式的线性组合。
• DEEP 多项式是什么？为何要构造它？答：将在下一小节简要说明。

3.2 DEEP 多项式

有了 2.3.3 的阐述，对于 DEEP 多项式就有比较清楚的认识了。实际上，没有 DEEP 多项式，从 Composition 多项式构造完毕开始，直接开始 FRI，并辅以 witness 与 constraints 的一致性检查，就完全可以称为一套证明系统了。

而运用了 DEEP-ALI 则如 2.3.3 与 2.3.4 所阐述，达到了一箭五雕的目的。

• 证明了 $z$ 处各值在对应的多项式上
• 证明了 $trace,composition$ 的一致性
• 证明了约束的成立
• 证明了 $trace$ 多项式是定义在 $F_q$ 上的，即：它的所有系数都是来自于 $F_q$。（具体方法参见3.8.2^[1]）
• 以上各项的概率都比上面的传统方法要强

这里有两点需要注意：

• 乍一看 DEEP 多项式的前面的求和项好似 $trace$ 多项式的线性组合，这是不了解时容易犯的错误。
• DEEP 多项式是三个商多项式的线性组合： $CompositionPolynomialTrace$，约束中出现的 $trace$，$trace$ 多项式为 $F_q$ 上而构造。

3.3 STARK 的安全性

3.3.1 DEEP + FRI 的安全性

所以对于STARK安全性的讨论就首先就要对 DEEP 多项式构造后的安全性的讨论。这里直接引用手册^[1]中的例子，并做简单的阐述。

这里只要明确几个问题就可以完全明白：

1. 作弊后如何通过 verifier 的检查？答：这要根据 verifier 的检查来分别讨论，一个是 DEEP 多项式自身值的一致性检查，一个是 FRI 的正确性。
2. 如何通过 FRI 测试？ 答：所有正式参与 FRI 的多项式都是“真”的。
3. 如何通过 DEEP 一致性的检查？ 答：只有一定的概率可以通过，参与 DEEP 值的计算的各个部分的值都是承诺过的。
4. 综合2，3，如果要伪造一个 $DEE{P}_{fake}$，它满足：
   • 在求值域 $D$ 的一个 $\rho -fraction$ 集合 $S$ 上与 $DEE{P}_{real}$ 值相等。这也达到了一个 $|S|-1$ 次多项式 $DEE{P}_{fake}$ 与一个高次多项式 $DEE{P}_{real}$ 交点个数的上限。（因为 $|S|=\rho |D|$，“真”多项式的次数是 $|S|-1$）
   • $DEE{P}_{fake}$ 必然能通过 FRI 测试。

综上，就很容易看出，在一次测试中，能通过 verifier 检查的概率就是 $\rho$。所以一次测试可以提供 $\log \frac{1}{\rho }$ bits 的安全性。假设测试需要进行 $l$ 次，那么就提供了 $$k(bitssecuritylevel)=\log \frac{1}{\rho }\ast l$$

3.3.2 grinding 安全性

这个过程和简单，大家很熟悉，就是证明在hash后要满足先导 0 的要求。其目的是通过增加造假的计算代价，来减轻 $l$ 的压力。而由于该过程只能 brute-force，因此设置几个先导 0 就是几个 bits security level。

3.3.3 STARK 安全性

所以，就基本可以看懂论文中如下公式：

参考文献

• [1] ethSTARK Documentation – Version 1.1
• [2] POLYNOMIAL CODES OVER CERTAIN FINITE FIELDS
• [3] Fast Reed-Solomon Interactive Oracle Proofs of Proximity
• [4] Worst-case to average case reductions for the distance to a code
• [5] DEEP-FRI: Sampling Outside the Box Improves Soundness

Cairo VM

Cairo VM 是一个非常精简的虚拟机模型，它没有类似于x86的通用寄存器（%eax, %ebx 等等），并且它仅仅只支持有限域Fp上加法和乘法 (p = 0x800000000000011000000000000000000000000000000000000000000000001)， 这篇文档提到了stark-curve 的参数设置。

Q1: 可能大家会好奇，仅仅只有加法、乘法，怎么就能够实现各种算术函数呢?

1. 减法：a - b = a + (b * (-1))
2. 布尔约束： a*(1-a) = 0
3. 布尔运算: a & b = a*b
4. 比特分解（bit-decompose）: 比如得到一个u32 的32个比特，a = \sum_{i=0}^{31} 2^i * a_i；当然有更好的方法来实现这个功能，如使用builtin()。

Cairo 的加法指令和乘法指令的操作数都在内存上，Cairo 的内存比较特殊，是只读的（immutable）。这和大部分的虚拟机都不一样，比如：

• EVM 的操作数通常是放在 stack 上，而 stack 是可以修改的；
• x86 架构的操作数是在通用寄存器中。

大家可能会好奇，那么如何实现赋值（assignment）呢？

需要为赋值语句的左侧的变量 lhs 分配一个新的内存，然后使用assert_eq 建立这个新变量 lhs 与旧变量 rhs 之间的相等关系。

我们举个例子来说明，比如：

# equivalent to assert_eq(b, 3)
b = 3 

# equivalent to assert_eq(a, b+1)
a = b+1

# will alloc a new memory space for `a`(we call it `a2`) on the left side
# equivalent to assert_eq(a2, a+15)
a = a + 15

Cairo VM Instruction Set

Cairo VM 的指令集是

• assert_eq：实现算术表达式；

  一个复杂的算术表达式会对应多条 VM 指令；例如，

  y = x^3 + 23*x^2 + 45*x + 67
  
  # the above compound expression is equivalent to 5 bytecodes, they cost 5 memory slots
  # 1*x+23
  [ap] = [ap-1] + 23; ap++ 
  # (1*x+23)*x
  [ap] = [ap-1]*[ap-2]; ap++ 
  # (x+23)*x + 45
  [ap] = [ap-1] + 45; ap++ 
  # ((x+23)*x + 45)*x
  [ap] = [ap-1]*[ap-4]; ap++
  # ((x+23)*x + 45)*x + 67
  [ap] = [ap-1] + 67; ap++
  

• call/ret: 函数调用

• jmp/jmpi: 条件跳转，用于支持控制流

在本节，我会以 call/ret 为例，讲解一下Cairo VM指令集如何支持 函数调用 这一实用功能。

• 假设，函数A 的栈帧指针（stack frame pointer）为 fp；

• 假设，函数B 在执行到call B 之前的 allocation pointer 为 ap；

• 函数 B 的栈帧指针为 new_fp = ap + 2；

• 在函数 A 中调用函数 B 之前，需要先把入参放到 [new_fp - 3], [new_fp - 4], ...等区域中；

• 将函数 A 的stack frame pointer 的值保存到 [new_fp-2]

• 将函数 A 中在call 指令之后的那条指令的地址保存到[new_fp-1]

• 当函数 B 结束执行之后，就可以通过读取[new_fp - 1] 然后更新 pc ，读取 [new_fp-2 来更新fp，回到函数 A 的执行。

以下图所示的函数调用示例，函数 f 调用了函数 g，函数g 调用了两次 h。需要注意的是，调用两次 h，产生的栈帧并没有重合（通常在x86架构中，它们的栈帧是要重合的）。

上述示例调用的栈帧如下图所示。

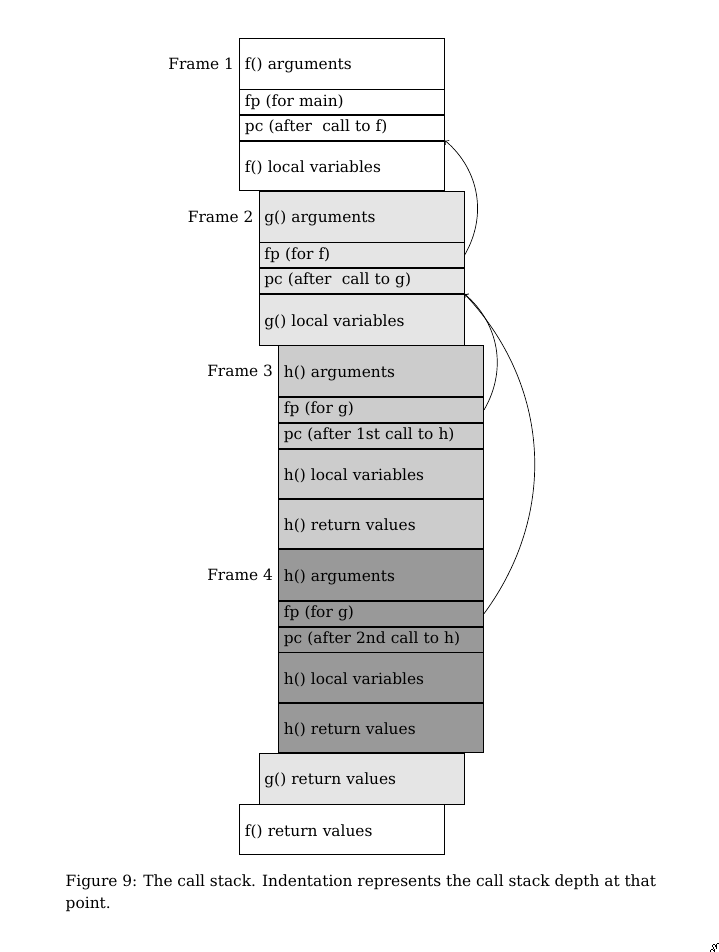
更多技术细节，大家可以看一下 Cairo VM 的白皮书^[1]。

Cairo 语言

从以上对 Cairo VM 的介绍，大家不难发现，Cairo 汇编代码其实比较简陋，我们开发者不可能手写Cairo assembly code。所以，我们在开发真实应用时，使用的是 cairo 语言，这个语言的词法形式与python类似。

参考资料

1. Cairo VM whitepaper

Cairo开发流程示例

概述

学习Cairo开发主要有2个资料，一个是官方提供的学习文档，另一个则是官方提供的playground。 本文将主要概念和开发流程简要介绍，同时附上案例。

基本概念

1. StarkNet - 一个无需许可的去中心化 ZK-Rollup，作为以太坊上的 L2 网络运行，任何 dApp 都可以在不影响以太坊的可组合性和安全性的情况下实现无限规模的计算。

2. Cairo - 一种编程语言用于可被证明程序的编写，使得其他验证者确信该程序被正确执行。StarkNet的基础设施及其合约都是使用Cairo编写的。

3. 内存模型 - 支持只读的非确定性内存，这意味着每个内存单元的值由证明者选择，但它不能随时间改变（在 Cairo 程序执行期间）。我们使用语法 [x] 来表示地址 x处的内存值。例如，如果我们在程序开始时断言 [0] = 7，那么在整个运行期间 [0] 的值将是 7。

4. Assert - 断言声明，assert <expr0> = <expr1>，在Cairo中有2个用处：一是验证左右2边的值是否相同；二是给内存单元设置值，如“内存模型”中的例子。

5. 递归，而非循环 - 由于内存模型的不可变性，需要使用递归实现循环的功能。

6. 类型felt - field element，整型，范围在-P/2 < x < P/2，其中P的取值（StarkNet实现时）是质数2^251 + 17*2^192 + 1

7. 除法 - 由于不支持浮点计算，因此有余数的情况下，是采用逆运算来记录结果的。例如，x = 7 / 3 ，将记录为一个felt满足3 * x = 7，原理是当3 * x的结果超出felt取值范围后，会自动将为7。因此，下面y的结果还是7，而不是6。

x = 7 / 3
y = x * 3

8. 内存分配 - 使用标准库函数alloc()来分配一个新的内存段。实际上，分配内存的确切位置只有在程序终止时才会确定，这样可以避免指定分配的大小。

9. 提示(hint) - 提示是一段Python代码，其中包含只有证明者才能看到和执行的指令。从验证者的角度来看，这些提示是不存在的。

func bar() -> (res):
    alloc_locals
    local x
    %{ ids.x = 5 %}  # Note this line.
    assert x * x = 25
    return (res=x)
end

%{ %}括起来的部分提示，其含义就是将5赋值给ids.x，也就是在上面1行语句local x申请的x。 * 作用： 提示有助于处理程序输入的方式——证明者必须知道要处理哪个输入，但验证者并不关心（验证者只关心初始状态以及解决方案是否有效）。 换句话来说，提示是不需要被用于生成执行轨迹和定义约束的，因此，如何充分利用提示及其他方法来缩短执行轨迹、减小内存模型来优化Cairo程序显得非常重要，这关系着系统的执行时间和需支付的gas费用。

开发流程

Cairo目前，有3种开发模式：本地开发测试，面向以太坊的部署开发和面向StarkNet的部署开发。其中本地模式，可以使用提示，无需部署合约。而其他2种则需要部署在相应网络上，只能使用官方指定的包含了提示的基本函数库。

1. 本地开发测试模式

   1. 创建Cairo文件(例如puzzle.cairo)，编写合约
   2. 执行编译命令

   	cairo-compile puzzle.cairo --output puzzle_compiled.json
   

   3. 执行执行命令，具体参数可以查看帮助文档

   	cairo-run --program=puzzle_compiled.json \
   		--print_output --layout=small \
   		--program_input=puzzle_input.json
   

2. 面向StarkNet的部署开发

   1. 创建Cairo文件(例如puzzle.cairo)，编写合约
   2. 执行编译命令，确保没有bug

   	starknet-compile puzzle.cairo --output puzzle-compiled.json --abi puzzle-abi.json
   

   3. 创建py文件，编写部署、测试代码

   @pytest.mark.asyncio
   async def test_arithmetic():
       # 创建用于StarkNet系统的模拟器
       starknet = await Starknet.empty()
   
       # 部署合约，puzzle.cairo
       contract = await starknet.deploy(
           source=CONTRACT_FILE,
       )
   
       # 调用puzzle中的对外暴露的方法
       x = 3; y = 14;
       response = await contract.recursive_calc_pow(x, y).call()
       assert response.result[0] == (x ** y) % P
   

   4. 执行python文件

此外，还可以参考命令行模式下部署合约、调用合约的方式。

注意事项

1. 内建指令: %builtins。 须在程序开始导入，例如，output

2. 隐式参数及调用：隐式参数可以显示调用或者隐式调用。 main函数隐式调用；func_abc函数显示调用

%builtins output

func main{output_ptr : felt*}(){output_ptr : felt*}:
	res = func_abc{output_ptr = output_ptr}()
...

3. 使用提示，需在提示的外部，即验证者能执行的部分，对提示修改的数据进行校验。

4. return () 的有() ,其中可以放返回值。

有用信息

StarkNet Alpha on Mainnet

• StarkNet的核心合约地址： 0xc662c410C0ECf747543f5bA90660f6ABeBD9C8c4
• 顺序器 URL: https://alpha-mainnet.starknet.io

StarkNet Alpha version 4 on Goerli

• StarkNet的核心合约地址： 0xde29d060D45901Fb19ED6C6e959EB22d8626708e
• 顺序器 URL: https://alpha4.starknet.io

Cairo案例

实现pow

%lang starknet

from starkware.cairo.common.math import abs_value, assert_nn, assert_le, sqrt, unsigned_div_rem, signed_div_rem
from starkware.cairo.common.math_cmp import is_le, is_nn, is_in_range
from starkware.cairo.common.pow import pow
from starkware.cairo.common.serialize import serialize_word

func recursive_calc_pow{range_check_ptr}(x, p) -> (y):
    alloc_locals

    if p == 0:
        return (1)
    end

    if p == 1:
        return (x)
    end

    let (div, rem) = unsigned_div_rem(p, 2)

    let (local res) = recursive_calc_pow(x * x, div)

    if rem == 1:
        return (res * x)
    end

    return (res)
end

这里使用了2分递归的方式实现pow的求解。

StarkDEX Deep Dive: the STARK Core Engine

引言

(译者按：本文翻译自Medium中的同名文章)

这是深入了解StarkDex系列的第三部份。我们在这个系列介绍一个通用的STARK证明系统，当中包括StartDex。如果你还没有对StarkDEX的整体了解，建议先阅读第一部份及第二部份，你亦可独立阅读本文。我们亦建议你阅读 Stark数学系列，当中深入讨论本文中的数学架构。

本文中，我们形容STARK证明系统为一个证明者(prover)和验证者(verifier)之间的交互式协议。证明者发出一系列的讯息试图说服验证者一个特定的计算己被正确地执行(已验证陈述)。验证者则以随机数回应该讯息。最后，如果计算真的被正确执行，验证者会接受该证明；否则，验证者(有很高概率)拒绝接受。

注意，这里我们形容Stark系统为一个交互式协议，在Alpha版本的StarkDEX，非交互式系统最终会取代交互式系统。在非交互式系统，证明者提供一个证明后，验证者直接决定是否接受。

STARK证明系统

想重温执行追踪(execution traces)及多项式约束(polynomial constraints)，可阅读Stark数学系列中算术化(Arithmetization)一及二。

轨迹

一个计算的执行轨迹，或简称轨迹，是一个机器状态的序列 — 每个时钟周期一个。如果一个计算需要 w 个寄存器和 N 个周期，执行轨迹可表达为一个 N x w 的表。要证明一个有关计算正确性的陈述，证明者首先要计算出一个轨迹。

将轨迹的列表达为f₁, f₂,…, fs 。每一个 fⱼ 的长度都是N=2ⁿ ，n是一个固定的值。 轨迹单元内的值是一个大域F的元素。在Alpha 版本，Ｆ是一个252 位的质数域。轨迹求值域定义为 ，其中 g 是 F 的乘法群的子群中的生成元。 实际上，我们以 的元素去代表轨迹的行。 每个轨迹列被视为在轨迹求值域上对次数小于 N 的多项式的 N 次逐点求值。这些多项式可被称为轨迹列多项式(trace column polynomials)，或简称列多项式(column polynomials)。

轨迹低度扩展 (Trace Low Degree Extension) 及承诺 (Commitment)

如前所述，每个轨迹行可视为一个度数低于Ｎ的Ｎ求值。要达至一个安全的协议，每个这样的多项式都要在一个更大的域求值，该域称为求值域(evaluation domain)。例如，在StarkDex Alpha，求值域的大小通常是16*N。我们称这个求值为轨迹低度扩展(Low Degree Extension, LDE)，而求值域与轨迹域之间的比例称为爆炸倍数 (熟悉编码理论的人会发现爆炸倍数是 1/rate，而LDE实际上是轨迹的里德-所罗门编码(Reed-Solomon code))。

证明者在产生轨迹LDE后，将其承诺。整个系统，承诺通过建立一系列域元素的默克尔树(Merkle tree)来实现，默克尔树的根会发送到验证者。后者涉及几个工程学上的考虑，包括域元素序列化及哈希函数的选择－为令文章更简洁，详情在此略过。

有关默克尔树叶子的选择，如果一个承诺打开可能牵涉多个域元素，它们最好集中在同一个默克尔树叶子。在轨迹LDE的情况，这意味着所有轨迹LDE“列”(所有在gⁱ点的行多项式的求值) 的域元素会被集中在同一个默克尔树叶子。

约束

一个执行轨迹只在符合以下条件才成立：(1)某些边界约束成立，及(2)每对连续状态都满足计算规定的约束。例如，在某一时间点 t，第一个和第二个寄存器的内容相加，把结果放在第三个寄存器，相关的约束是： $Trace[t,1]+Trace[t,2]-Trace[t+1,3]=0$　。

当且仅当计算正确时，约束表示为轨迹单元上组成的多项式。因此，它们被称为轨迹的代数中间表示多项式约束 (Algebraic Intermediate Representation, (AIR) Polynomial Constraints)。例如，证明去中心化交易所(Decentralized Exchange, DEX)执行的一批交易的正确性时，约束成立当且仅当这批交易都有效。

以下看看几个不同的约束例子：

1. f₂(x)-a = 0 for x=g⁷ (第二列第 g⁷ 行的值等于 a)
2. f₆²(x) -f₆(g³x) = 0 for all x (每行第六列的值的平方等于三行前的值)
3. f₃(x) -f₄(gx) = 0 for all x but g⁵ (每行第三列的值等于前一行第四列的值，除了第g⁵行外)
4. f₂(x) -2*f₅(x) = 0 for all x in an odd row (奇数行第二列的值等于该行第五列的值的双倍)

我们的目标是证明一个计算是否正确。写出一套当且仅当计算有效才成立的多项式约束，我们把原本的问题简化成证明多项式约束成立。

由多项式约束至低度测试问题

接下来，我们将每项约束表达成一个有理函数。上面的约束(1)翻译成

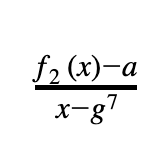
这个多项式的度数最高为 deg(f₂)-1 当且仅当约束(1)成立 (详情参看 Arithmetization 1）。要明白约束(2), (3)和(4)，首先回忆一下以下集合{x∈ F | xᴺ-1=0} 正好等于乘法群F 中的所有 x 。所以，我们得出以下的简化结果：

• 约束(2)成立当且仅当以下有理函数是一个度数最多为2*deg(f₆)-N的多项式：

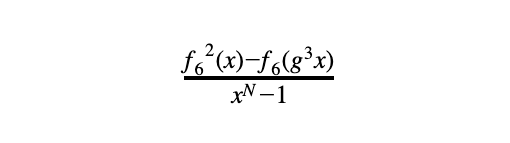
• 约束(3)成立当且仅当以下有理函数是一个度数最多为max{deg(f₃), deg(f₄)} — N+1的多项式：

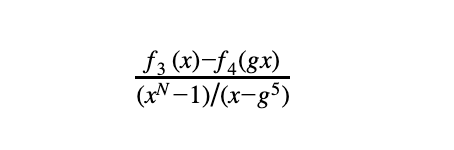
• 约束(4)成立当且仅当以下有理函数是一个度数最多为max{deg(f₂), deg(f₅)} — N/2的多项式：

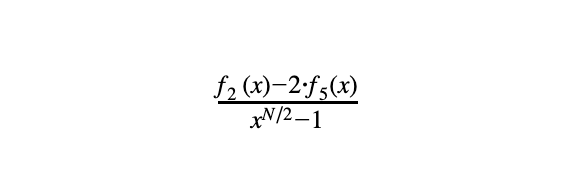
当约束表达成有理函数时，分子定义了需要在轨迹执行的规则；分母则定义相关规则应该成立的域。由于验证者需要求这些有理函数的值，STARK系统的简洁非常重要，分母定义的域需要被快速地求值，如上述四个例子。

组合多项式

为了高效地证明执行轨迹的有效性，我们力图达到以下三个目标：

1. 在轨迹多项式之上构建约束。
2. 调整不同度数的约束至同一度数，以令它们可以合拼成一个该度数的多项式。
3. 合拼所有约束至一个(更大的)多项式，称为组合多项式，使得只要一个低度数测试即可证明所有约束的(低)度数。

本节讨论以上如何实现。

度数调整

要确保可靠性，我们要显示所有以轨迹列多项式建构的所有约束都是低度数。因此，我们把约束的整体度数调整为所有约束之中最高的一个，称为D (如果D不是2的幂，则向上调整至最接近的2的幂)。D即为组合多项式的度数。

度数调整方法如下：

给定一个度数 Dⱼ 的常数 Cⱼ(x)，我们以以下形式加进组合多项式

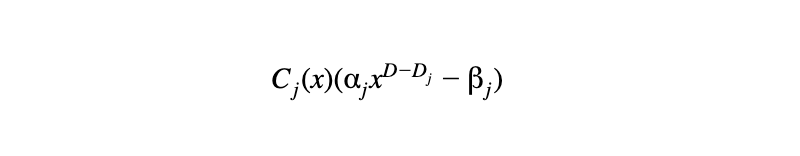
当中𝛼ⱼ 及 βⱼ 是验证者发来的随机域元素。结果，如果组合多项式是低度数，每个独立约束便会自动是低度数。结果是一个以下形式的组合多项式。

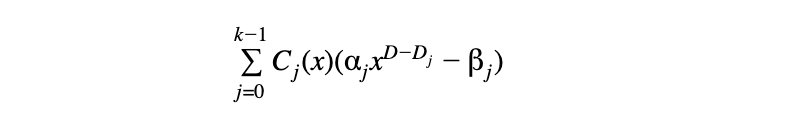
当中k是常数。

约束组合

一旦证明者已承诺轨迹 LDE，验证者将提供随机系数以创建约束的随机线性组合，从而产生合成多项式。无需单独检查每个约束在轨迹元素上的一致性，只需对组合多项式应用低度测试即可，该组合多项式表示一次应用于所有轨迹的所有约束。

由于我们的 Alpha 版本中使用的约束为 2 度或以下，因此组合多项式的度数为 2N。我们可以将组合多项式 H(x) 表示为长度为 2N 的单列求值，或者，我们更倾向将其表示为长度为 N 的两列 H₁(x) 和 H₂(x)，其中 H(x) =H₁(x²)+xH₂(x²)。

承诺组合多项式

接下来，证明者对H 1 和 H 2 的两个组合多项式列再次进行低度扩展。由于这些列与轨迹列的长度 N 相同，我们有时将它们称为组合多项式轨迹，并且我们以与执行轨迹多项式相同的方式进行扩展和承诺。这是通过将它们扩展相同的爆炸倍数来完成的，将同一行的域元素作为默克尔树的叶子，计算哈希值并将树的根作为承诺发送。

随机点的一致性检查（DEEP 方法）

注意，给定点（域元素）z 的 H(x) 值可以通过两种方式获得：从 H1(z²) 和 H2(z²) 或通过计算上述的约束线性组合。该计算在需要计算的轨迹列上产生一组点，以完成所需的计算。计算单个点的 H(x) 所需的点集称为掩码(mask)。因此，给定一个点 x=z，如果给定 H₁(z²) 和 H₂(z²) 的值以及轨迹上的对应的掩码值，我们可以检查 H 和轨迹之间的一致性。

在这个阶段，验证者发送一个随机采样的点 z∊F。证明者将 H₁(z²) 和 H₂(z²) 的求值连同计算 H(z) 所需相关元素的掩码的求值一起发回。用 {yⱼ} 表示证明者发送的这些值集。对于诚实的证明者，每个 yⱼ 的值等于 fₖ(zgˢ)，其中 k 是相应单元格的列，s 是其行偏移量。然后验证者可以通过两种方式计算 H(z)：基于 H1 和 H2（使用 H(z)=H1(z2)+z*H2(z2)）和基于掩码值 yⱼ。它验证两个结果是相同的。它还没证明证明者在这个阶段发送的值是正确的（即确实等于点 z 的掩码值），这将在下一节中完成。这种通过从一个大域中采样一个随机点来检查两个多项式之间一致性的方法称为DEEP（Domain Extension for Eliminating Pretenders）。感兴趣的读者可以在 DEEP-FRI 论文中找到更多细节。

DEEP 组合多项式

为了验证证明者发送的 DEEP 值是否正确，我们创建了第二组约束，然后将其转换为类似于上面定义的组合多项式的低度测试问题。

对于每个值 yⱼ，我们定义以下约束：

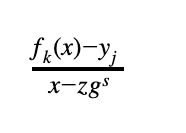
有理函数是度数 deg(fₖ)-1 的多项式当且仅当 fₖ(zgˢ) = yⱼ。用 M 表示掩码的大小。验证者从域中抽取 M+2 个随机元素 {𝛼ⱼ}ⱼ 。我们将用作为低度测试的多项式称为 DEEP 组合多项式。定义如下：

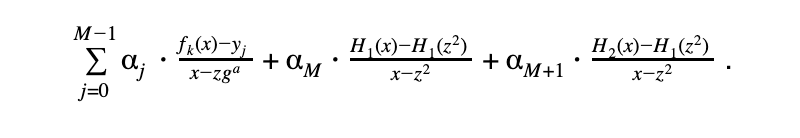
（注意，在第一项中，k 和 zgˢ 不是常数，而是取决于 j）。这是如下形式的（随机）线性组合：

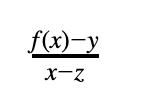
其中 f 是轨迹多项式或 H₁ / H₂ 多项式。因此，证明这种线性组合是低度的意味着证明轨迹多项式的低度以及 H 1 和 H 2 多项式的低度，以及 DEEP 值是正确的。

低度测试

低度测试的 FRI 协议

对于低度测试，我们使用称为 FRI（代表 Fast Reed-Solomon Interactive Oracle Proof of Proximity）协议的优化变体，感兴趣的读者可以在这里阅读更多相关信息。相关的优化在下文详述。

如我们关于该主题的文章所述，该协议由两个阶段组成：承诺阶段和查询阶段。

承诺阶段

在基本的 FRI 版本中，证明者将原始的 DEEP 约束多项式，这里表示为 p₀(x)，分成两个度数小于 d/2 的多项式，g₀(x) 和 h₀(x)，满足 p₀(x)=g₀ (x²)+xh₀(x²)。验证者采样一个随机值𝛼₀，将其发送给证明者，并要求证明者承诺多项式 p₁(x)=g₀(x) + 𝛼₀h₀(x)。注意，p₁(x) 的度数小于 d/2。

然后我们通过将 p₁(x) 拆分为 g₁(x) 和 h₁(x) 继续递归，然后选择一个值 𝛼₁，构造 p₂(x) 等等。每次，多项式的度数减半。因此，在 log(d) 步骤之后，我们得到了一个常数多项式，证明者可以简单地将常数值发送给验证者。

正如读者所预料的那样，上述多项式求值的所有承诺都是通过使用上述默克尔承诺方案做出的。

为了使上述协议起作用，我们需要一个性质：对于域 L 中的每个 z， -z 也要在 L 中的。此外，p₁(x) 上的承诺不会超过 L，但是超过 L²={x² : x ∊ L}。由于我们迭代地应用 FRI 步骤，L² 还必须满足 {z, -z} 属性，依此类推。通过我们选择使用乘法陪集作为我们的求值域来满足这些代数要求。

查询阶段

我们现在须检查证明者没有作弊。验证者对 L 中的一个随机 z 进行采样并查询 p₀(z) 和 p₀(-z)。这两个值足以确定 g₀(z²) 和 h₀(z²) 的值，从以下两个“变量”g₀(z²) 和 h₀(z²) 中的两个线性方程可以看出：

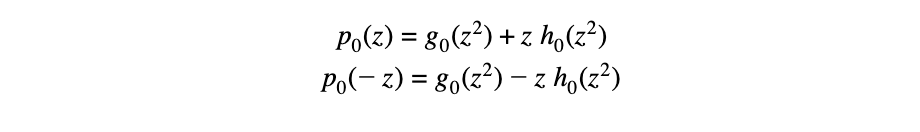
验证者可以求解这个方程组并推导出 g₀(z²) 和 h₀(z²) 的值。因此它可以计算 p₁(z²) 的值，它是两者的线性组合。现在验证者查询 p₁(z²) 并确保它等于上面计算的值。这表明证明者在承诺阶段发送的对 p₁(x) 的承诺确实是正确的。验证者可以继续，通过查询 p₁(-z²)（回想一下(-z²)∊ L² 并且 p₁(x) 上的承诺是在 L²) 上给出的，并从中推导出 p²(z⁴)。

验证者以这种方式继续，直到它使用所有这些查询最终推导出 P_h(z) 的值，当中 h=log(d)。但是，回想一下，P_h(z) 是一个常数多项式，其常数值是由证明者在承诺阶段（在选择 z 之前）发送的。验证者应检查证明者发送的值是否确实等于验证者从对先前函数的查询中计算出的值。

验证者收到的所有查询回应也需要与证明者在承诺阶段发送的默克尔承诺进行一致性检查。因此，证明者将解除承诺信息（默克尔路径）与这些回应一起发送，以允许验证者执行此操作。

此外，验证者还必须确保 p0 多项式与衍生出它的原始轨迹（fⱼ 和 Hⱼ）之间的一致性。为此，对于查询阶段的两个查询值 p₀(z) 和 p₀(-z) 之一，证明者还将由 DEEP 组合多项式归纳的 fⱼ 和 Hⱼ 的值连同它们的解除承诺一起发送。然后，验证者检查这些值与跟踪上的承诺的一致性，计算 p₀ 的值并检查它与证明者发送的值 p₀(z) 的一致性。

为了达到协议所需的健全性，查询阶段会重复多次。对于 2ⁿ 的放大系数，每个查询大致贡献了 n 位安全性。

转换为非交互式协议 (Fiat-Shamir)

到目前为止，上述协议被描述为交互协议。在我们的 Alpha 版本中，我们将交互式协议转换为非交互式版本，以便证明者以文件（或相等的二进制表示）的形式生成证明，验证者接收它以验证其正确性（链上）。

通过 BCS 构造来消除交互性，这是一种将交互式 Oracle 证明 (IOP)（例如上述协议）与密码哈希函数相结合以获得密码证明的方法。有关此机制的一些背景信息，请参阅我们的博客文章。

这种结构背后的基本思想是证明者模拟从验证者那里接收随机性。 这是通过从哈希函数中提取随机性来完成的，该哈希函数应用于证明者发送的先前数据（并附加到证明中）。这种结构通常被称为哈希链。在我们的 Alpha 版本中，哈希链是通过对证明者和验证者都知道的公共输入进行哈希来初始化的。为了简单起见，省略了进一步的技术细节。

证明长度优化

除了上述协议的描述外，我们还采用了几种优化技术来减少证明大小。这些技术将在以下小节中描述。

FRI 层跳过

在 FRI 协议的承诺阶段，证明者可以跳过 FRI 层并仅在其中的一个子集上承诺，而不是在每个 FRI 层上承诺。这样做，证明者减少了一些默克尔树的创建，这意味着在查询阶段它有更少的解除承诺路径发送给验证者。不过，这里有一个权衡。例如，如果证明者只是每三层承诺一次，为了回答查询，它需要在第一层的 8 个元素解除承诺（而不是在标准情况下发送的 2 个）。证明者在承诺阶段考虑了这一事实。它将默克尔树的每个叶子中的相邻元素打包在一起。因此，跳过层的成本是发送更多的域元素，而不是更多的身份验证路径。

FRI 最后一层

另一个用于减少证明大小的 FRI 优化是在最后一层达到常数值之前终止 FRI 协议。在这种情况下，证明者不会发送最后一层的常数值作为承诺，而是发送代表最后一层的多项式的系数。这允许验证者像以前一样完成协议，而无需承诺（并为较小的最后层中的域元素发送解除承诺）。在我们的 Alpha 版本中，FRI 承诺阶段通常在达到小于 64 次的多项式 pⱼ 时终止。确切的数字可能因轨迹大小而异。

Grinding

如上所述，每个查询都会为证明的安全性（健全性）添加一定数量的位。然而，这也意味着证明者会发送更多的解除承诺，这会增加证明的大小。减少查询需求的一种机制是增加恶意证明者生成虚假证明的成本。我们通过在上述协议中添加一个要求来实现这一点，即在证明者做出的所有承诺之后，它还找一个 256 位随机数与哈希链的状态一起哈希，生成所需长度的预定义模板。模板的长度定义了证明者在生成表示查询的随机性之前必须执行的一定量的工作。结果，试图生成有利查询的恶意证明者将需要在每次更改承诺时重复grinding过程。另一方面，诚实的证明者只需要执行一次grinding。

在我们的 Alpha 版本中，我们使用具有特定模式的模板，其中包含已执行grinding的位数和固定模式。这类似于在许多区块链上执行的grinding。证明者找到的 nonce 作为证明的一部分发送给验证者，然后验证者通过运行一次哈希函数来检查其与哈希链状态的一致性。

在我们的 Alpha 版本中，证明者需要执行 32 位grinding。因此，可以减少达到若干安全级别所需的查询数量。爆炸倍数为 2⁴，这允许将查询数量减少 8。

用于grinding的位数作为参数传达给验证者。如果证明与该参数不一致，验证者将拒绝该证明。

周期列

许多密码原语涉及使用一些列表常数。当我们多次应用相同的密码原语时，我们会得到一个周期性的常数列表。在 AIR 中使用此列表的一个选项是将其值添加到轨迹中并提供保证其值正确的约束。但是这造成浪费，因为验证者知道该列表的值，因此计算 LDE 并承诺它们是没有意义的。相反，我们使用一种我们称为周期列的技术。每个这样的列的周期结构产生可以简洁地表示的列多项式。在多项式的经典表示，a₀+a₁x+a₂x²+…aₙ*xⁿ ，其系数 (a₀,…,aₖ) 的向量的简洁表示意味着大多数 aⱼ 为零。这使验证者能够有效率地计算这些多项式的逐点求值。

总结

StarkDEX 系统使用的通用 STARK 证明系统的描述到此结束。 所描述的 STARK 证明系统保留了已知的好处，例如透明度（消除了受信任的设置）、高度可扩展的验证和后量子安全性。 最重要的是，它包括几个创新的贡献和优化，显着减少了证明的大小，并以以前文献中没有描述的方式增强了有效可证明陈述的表达能力。

在本系列的下一篇也是最后一篇文章中，我们将描述我们如何为 StarkDEX 构建 AIR（Algebraic Intermediate Representation）。与往常一样，如果您有任何问题或意见，请在此处或在推特 @StarkWareLTD 上与我们联系。

Kineret Segal & Gideon Kaempfer

StarkWare